Tangent bisectors
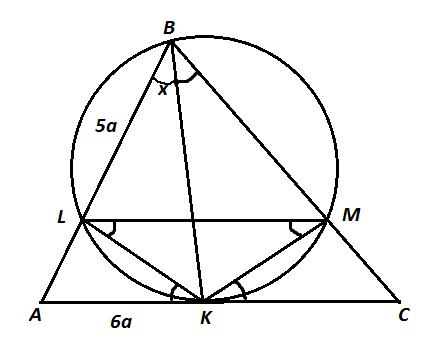 In a triangle
A
B
C
,
B
K
is an angle bisector. A circle with radius
3
5
passes through the vertex
B
, intersects
A
B
at a point
L
,
and is tangent to
A
C
at
K
. It is known that the length of
A
C
is
3
3
,
and the ratio of the lengths
∣
A
K
∣
to
∣
B
L
∣
is
6
:
5
. The area of the triangle
A
B
C
can be written as
c
a
b
, where
a
and
c
are coprime positive integers, and
b
is not divisible by the square of any prime. What is the value of
a
+
b
+
c
?
In a triangle
A
B
C
,
B
K
is an angle bisector. A circle with radius
3
5
passes through the vertex
B
, intersects
A
B
at a point
L
,
and is tangent to
A
C
at
K
. It is known that the length of
A
C
is
3
3
,
and the ratio of the lengths
∣
A
K
∣
to
∣
B
L
∣
is
6
:
5
. The area of the triangle
A
B
C
can be written as
c
a
b
, where
a
and
c
are coprime positive integers, and
b
is not divisible by the square of any prime. What is the value of
a
+
b
+
c
?
The answer is 64.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
First, assume that, the circle intersect the line B C at M , and then define O is the center of circle. I will divide into many steps.
1 . Proof that L M ∥ A C . Proof : Since the line A C tangent the circle at K . So, power point in A and C . We obtain that :
A K 2 = A L ( A B ) … … ( 1 ) C K 2 = C M ( C B ) … … ( 2 )
In the other hand, since B K is angle bisector. We obtain that, by angle bisector theorem, that is :
A K . B C = C K . A B ⟹ C K A K = C B A B … … ( 3 )
Then, divide equation ( 1 ) into ( 2 ) , we obtain : B K 2 A K 2 = C M ( B C ) A L ( A B ) , combine with equation ( 3 ) , obatain that
B C 2 A B 2 = C M ( B C ) A L ( A B ) ⟹ B C A B = C M A L ⟹ A L A B = C M B C ⟹ A L A L + B L = C M B M + C M ⟹ A L B L = C M B M . Implies that, since ∠ A B C = ∠ L B M , that is △ A B C ∼ △ L B M . Implies that L M ∥ A C .
2 . Find the length of L M . From the problem, we can assume that A K = a , then, B L = 6 5 . A K = 6 5 a . From, the equation ( 1 ) , and solve the equation by putting the values of A K and B L , we obatin that A L = 3 2 a . Then, by similarity, obtain that :
A C L M = A B B L ⟹ 3 3 L M = 2 3 a 6 5 a ⟹ L M = 3 5 3 .
Assume that B K intersect L M at N . Then, assume that ∠ A B C = α . We obtain that,
∠ M O K = ∠ L O K = 2 ∠ A B K = ∠ A B C = α .
It's easy to see that L N = N M , since L O M is isosceles triangle. And, since O K ⊥ A C , then O K ⊥ L M , since A C ∥ L M . Then,
3 . Find the length of N K . So, See the right triangle O M N , then, we obtain
sin α = sin ( ∠ N O M ) = O M N M = 3 5 6 5 3 = 2 1 3 , then, 2 1 = cos α = O M O N = 3 5 O N , then O N = 6 5 . So,
N K = O K − O N = 3 5 − 6 5 = 6 5
4 . Find the height of triangle A B C . Assume that B P is height of triangle A B C . Then, assume that B P intersect at L M at Q . Then, it's easy to see that P Q ∥ N K , implies B Q = N K = 6 5 . Since, B K ⊥ L M and B Q ⊥ L M . So, by similarity we obtain :
Q P B Q = Q P B Q ⟹ 3 2 6 5 = 6 5 h − 6 5 ⟹ h = 8 1 5
5 . Find the area of triangle A B C [ A B C ] = 2 1 . A C . B P = 2 1 . 3 3 . 8 1 5 = 1 6 4 5 3 .
So, a + b + c = 4 5 + 3 + 1 6 = 6 4
Let ∠ A B K = α and ∠ L B O = β (where O is the center of the circle passing through B , K and L ), then we can calculate the following angles in terms of α and β : ∠ A K L = α , ∠ B A C = 9 0 − 2 α + β , ∠ A K B = 9 0 + α − β , ∠ A C B = 9 0 − β .
Notice that the two triangles △ A B K and △ A K L are similar, hence: A K 2 = A B × A L = A B ( A B − B L ) = A B 2 − 6 5 A B × A K , which can be solved to obtain A K = 3 2 A B .
Apply the law of sines on △ A B K and recall that ∠ A B K = α and ∠ A K B = 9 0 + α − β : A B × sin ( α ) = A K × sin ( 9 0 + α − β ) = 3 2 A B × cos ( β − α ) , thus 2 3 sin ( α ) = cos ( β − α ) .
Next, apply the law of sines on △ B L O and recall that ∠ L B O = β : B L × sin ( β ) = O L × sin ( 1 8 0 − 2 β ) = O L × sin ( 2 β ) , thus B L = 3 1 0 cos ( β ) , and hence A K = 5 6 B L = 4 cos ( β ) .
Lastly, apply the law of sines on the two triangles △ A B K and △ B C K and recall that ∠ A B K = ∠ C B K = α , ∠ B A C = 9 0 − 2 α + β , ∠ A C B = 9 0 − β : sin ( 9 0 − 2 α + β ) × A K = sin ( α ) × B K = sin ( 9 0 − β ) × C K , thus c o s ( 2 α − β ) × A K = cos ( β ) × ( 3 3 − A K ) .
Now recall that 2 3 sin ( α ) = cos ( β − α ) and A K = 4 cos ( β ) , we obtain: 3 3 = 4 cos ( 2 α − β ) + 4 cos ( β ) = 8 c o s ( α ) cos ( α − β ) = 8 cos ( α ) 2 3 sin ( α ) = 6 sin ( 2 α ) , which yields 2 α = 6 0 ∘ , α = 3 0 ∘ .
We calculate the area of the triangle △ A B C : A r e a ( △ A B C ) = 2 1 A B × A C × sin ( ∠ B A C ) = 2 1 × ( 2 3 × 4 cos ( β ) ) × 3 3 × cos ( 6 0 ∘ − β ) = 2 9 3 ( cos ( 6 0 ∘ ) + cos ( 6 0 ∘ − 2 β ) ) = 2 9 3 ( 2 1 + 2 cos 2 ( 3 0 ∘ − β ) ) − 1 )
Suppose the circle, described in the problem, intersects B C at a point M . Suppose ∡ A B K = x . Because B K is an angle bisector, ∡ C B K = x . From the inscribed angle theorem, ∡ M L K = ∡ M B K = x . Because the circle is tangent to A C at K , ∡ A K L = ∡ L B K = x . Similarly, ∡ L M K = x and ∡ M K C = x .

The above implies that the line L M is parallel to A C . Note also that the triangles A K L and A B K are similar, so ∣ A K ∣ ∣ A L ∣ = ∣ A B ∣ ∣ A K ∣ . Because ∣ A K ∣ : ∣ B L ∣ = 6 : 5 , we can say that ∣ A K ∣ = 6 a , ∣ B L ∣ = 5 a for some positive length a . Then ∣ A K ∣ ∣ A L ∣ = ∣ A B ∣ ∣ A K ∣ can be rewritten as ∣ A L ∣ ⋅ ∣ A B ∣ = ∣ A K ∣ 2 , or ∣ A L ∣ ⋅ ( ∣ A L ∣ + 5 a ) = 3 6 a 2 . Solving this quadratic equation for ∣ A L ∣ , we get ∣ A L ∣ = 4 a or ∣ A L ∣ = − 9 a . ∣ Because ∣ A L ∣ > 0 , ∣ A L ∣ = 4 a .
The triangles A B C and L B M are similar, so ∣ L M ∣ = ∣ A C ∣ ⋅ ∣ A B ∣ ∣ L B ∣ = 3 3 9 5 = 3 5 3 . From the Sine Law, considering that the diameter of a circumscribed circle of L B M is 3 1 0 , sin ∠ L B M = 3 5 3 / 3 1 0 = 2 3 . So ∡ L B M = 6 0 ∘ and x = 3 0 ∘ .
Because ∣ L M ∣ = 3 5 3 and ∡ K L M = ∡ K M L = 3 0 ∘ , the altitude from K has length 2 1 ∣ L M ∣ ⋅ tan 3 0 ∘ = 6 5 . Because L M is parallel to A C and ∣ A B ∣ : ∣ A L ∣ = 9 : 4 , the altitude of the triangle A B C from B has length 4 9 ⋅ 6 5 = 8 1 5 . From this, the area of the triangle A B C is 2 1 ⋅ 3 3 8 1 5 = 1 6 4 5 3 . Therefore, the answer is 4 5 + 3 + 1 6 = 6 4 .
Although the point is not mentioned in the problem, the circle of radius 3 5 also intersects side B C at a point. We shall call that point M .
Now let A K = x and K C = 3 3 − x and we shall make the additional restriction that A K ≤ K C . By the given ratio, B L = 6 5 x . Through power of point, A K 2 = ( A L ) ( A B ) . Solving this relationship yields A L = 3 2 x and A B = 2 3 x .
Next, we proceed to angle chase. We see that ∠ B A C = ∠ B K M and ∠ B C A = ∠ B K L . However, since quadrilateral B M K L is cyclic, we have that ∠ B K M = ∠ B L M and ∠ B K L = ∠ B M L so L M is parallel to A C !
We can now use the fact that Triangle B L M is similar to Triangle B A C . Thus we have that 2 3 x 6 5 x = 3 3 L M , so L M = 3 5 3 . We are given that the radius of the circle is 3 5 so if we construct Triangle O L M , then we see that ∠ L O M = 1 2 0 ∘ . Thus, we get that ∠ A B C = 6 0 ∘ .
Since we have the value of ∠ A B C , we might expect to find the area of Triangle A B C by using 2 ( A B ) ( B C ) sin ∠ A B C ) . Now in order to do so, we must find the value of x .
Using the Angle Bisector Theorem we have that x 2 3 x = 3 3 − x B C . Evaluating yields B C = 2 9 3 − 2 3 x . With the same similar triangle relations as before, we get that B M = 2 5 3 − 6 5 x . Using Ptolemy's Theorem, we can find that B K = 2 5 . Now we use Law of Cosines on Triangle A B K to get that x = 2 3 3 − 7 since we wanted A K ≤ K C . Now we can use the area formula that was mentioned earlier. Plugging in the value for x , we get that the area is 4 9 3 − 3 7 4 9 3 + 3 7 2 3 2 1 which simplifies to 1 6 4 5 3 so our answer is 4 5 + 3 + 1 6 or 6 4 .