Tangent Circle
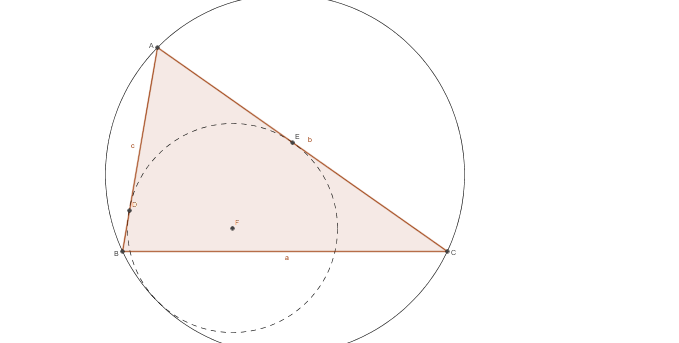
Let A B C be a triangle with sides A B = 7 , B C = 1 1 and C A = 1 2 , and let ω a be the circle tangent to A B , A C at the points D , E and internally tangent to the circumscribed circle ⊙ A B C . What is the length of the segment A D ?
Details and Assumptions
Assuming that the length of the segment A D is the simple fraction b a , type the sum a + b as your answer.
The answer is 33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I shall show a quick solution via flip inversion: We invert the diagram wrt circle centered at A with radius A B ⋅ A C , and then reflect it across the A -angle bisector. Then B would map to C , C would map to B , line A B maps to line A C , line A C maps to line A B , and the circumcircle of A B C is mapped to line B C . Tangency is preserved so ω A would map to the A -excircle and suppose its tangency point with line B C , C A , A B well be X , Y , Z respectively. Note that D , E map to Y , Z respectively. Then A B + A X = A B + B Z = A Z = A Y = A C + C Y = A C + C X , so we know the length of A to X along the perimeter of triangle A B C will be half the perimeter i.e. 1 5 , which is also the length of line segment A Y . Now by inversion A Y ⋅ A D = A B ⋅ A C = 8 4 and hence A D = 5 2 8 and the answer is 3 3 .
A synthetic solution:
Let X be point of tangency of both circles. Let Y and Z be midpoints of minor arcs A B and A C respectively. Now Y X ∩ A B = D , A C ∩ Z X = E , and Z B ∩ Y C = I where I is incenter of △ A B C . Thus Pascal's on cyclic hexagon A C Y X Z B implies points D , I , E collinear.
From this it becomes a routine length chase. A D = A E and A I ⊥ D E so we can construct P as shown in the diagram and we have r = s ( s − a ) ( s − b ) ( s − c ) = 5 3 2 and A P = 2 A B + A C − B C = 4 . so A I 2 = r 2 + A P 2 = 5 1 1 2 = A P ⋅ A E = 4 A D .
Thus A D = 5 2 8 , and 2 8 + 5 = 3 3 .