Tangent Circles

Similar solution with @Chirag Baliga ,s

Let the triangle be $ABC$ and its incenter be $I$ and inradius be $r$ . We note that $\sin \angle \frac B2 = \dfrac {IS}{IQ} = \dfrac {r-4}{r+4}$ , then $\cos \angle \frac B2 = \sqrt{1- \dfrac {(r-4)^2}{(r+4)^2}} = \dfrac {4\sqrt r}{r+4}$ . Similarly:

$\begin{cases} \sin \angle \dfrac A2 = \dfrac {r-1}{r+1} & \implies \cos \angle \dfrac A2 = \dfrac {2\sqrt r}{r+1} \\ \sin \angle \dfrac B2 = \dfrac {r-4}{r+4} & \implies \cos \angle \dfrac B2 = \dfrac {4\sqrt r}{r+1} \\ \sin \angle \dfrac C2 = \dfrac {r-9}{r+9} & \implies \cos \angle \dfrac C2 = \dfrac {6\sqrt r}{r+9} \end{cases}$ .

We note that:

$\begin{aligned} \angle \frac A2 + \angle \frac B2 + \angle \frac C2 & = 90^\circ \\ \angle \frac A2 + \angle \frac B2 & = 90^\circ - \angle \frac C2 \\ \sin \left(\angle \frac A2 + \angle \frac B2\right) & = \sin \left(90^\circ - \angle \frac C2\right) \\ \sin \angle \frac A2 \cos \angle \frac B2 + \sin \angle \frac B2 \cos \angle \frac A2 & = \cos \angle \frac C2 \\ \frac {r-1}{r+1} \times \frac {4\sqrt r}{r+4} + \frac {r-4}{r+4} \times \frac {2\sqrt r}{r+1} & = \frac {6\sqrt r}{r+9} \\ \frac {4r\sqrt r - 4\sqrt 4 + 2r\sqrt r - 8 \sqrt r}{(r+1)(r+4)} & = \frac {6\sqrt r}{r+9} \\ \frac {6\sqrt r (r-2)}{(r+1)(r+4)} & = \frac {6\sqrt r}{r+9} \\ (r-2)(r+9) & = (r+1)(r+4) \\ r^2 +7r-18 & = r^2 + 5r + 4 \\ 2r & = 22 \\ \implies r & = \boxed{11} \end{aligned}$

$SOLUTION:$

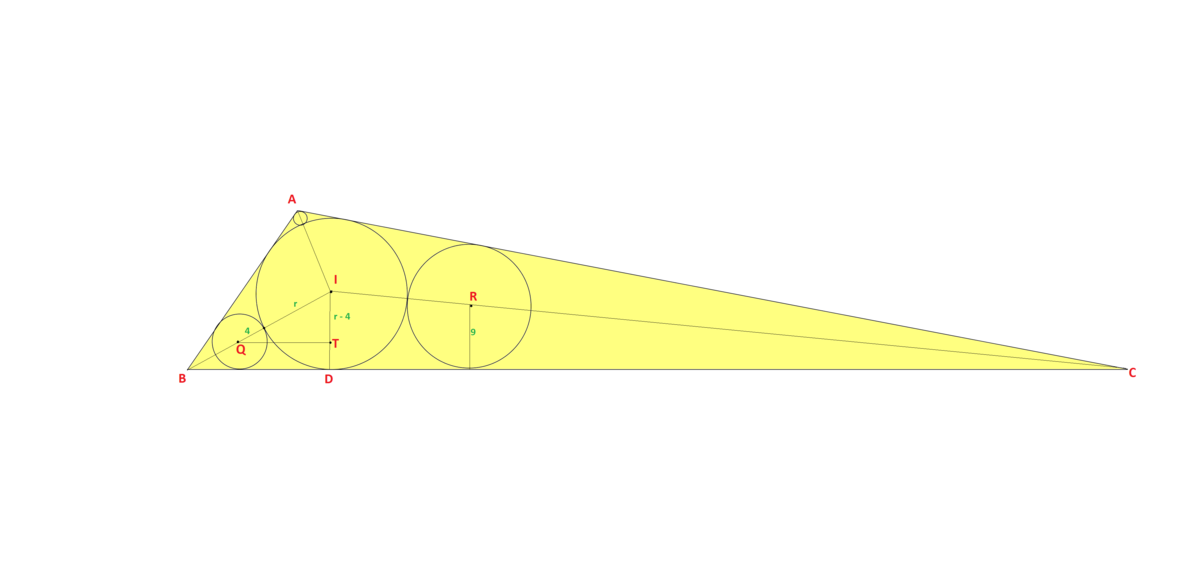
In $\triangle ABC$ let I be the incentre. Let the circles with radii 1,4 and 9 have centres $P , Q , R$ respectively.

$\angle IBD$ = $\angle IQT$ = $\frac{\angle B}{2}$

Then $\sin \frac{\angle B}{2}$ = $\frac{r - 4}{r+4}$

So 1 - $\sin \frac{\angle B}{2}$ = $\frac{8}{r+4}$

and 1+ $\sin \frac{\angle B}{2}$ = $\frac{2r}{r+4}$

So $\dfrac{1 - \sin \frac{\angle B}{2}}{1 + \sin \frac{\angle B}{2}}$ = $\frac{4}{r}$

But LHS = $\left(\dfrac{\cos\frac{\angle B}{4} - \sin \frac{\angle B}{4}}{ \cos \frac {\angle B}{4} + \sin \frac{\angle B}{4}}\right)^2$ $\Rightarrow$ $\left(\dfrac{1 - \tan \frac{\angle B}{4}}{1 + \tan \frac{\angle B}{4}}\right)^2$

Which is equal to $\tan^2 (\frac{\pi}{4} - \frac{\angle B}{4})$ . Therefore $\tan^2 (\frac{\pi}{4} - \frac{\angle B}{4})$ = $\frac{4}{r}$

Similarly $\tan^2 (\frac{\pi}{4} - \frac{\angle A}{4})$ .= $\frac{1}{r}$

and $\tan^2 (\frac{\pi}{4} - \frac{\angle C}{4})$ . = $\frac{9}{r}$

$(\frac{\pi}{4} - \frac{\angle A}{4})$ + $(\frac{\pi}{4} - \frac{\angle B}{4})$ + $(\frac{\pi}{4} - \frac{\angle C}{4})$ = $\frac{\pi}{2}$

Which implies $\tan (\frac{\pi}{4} - \frac{\angle A}{4})$ $\tan (\frac{\pi}{4} - \frac{\angle B}{4})$ + $\tan (\frac{\pi}{4} - \frac{\angle A}{4})$ $\tan (\frac{\pi}{4} - \frac{\angle C}{4})$ + $\tan (\frac{\pi}{4} - \frac{\angle B}{4})$ $\tan (\frac{\pi}{4} - \frac{\angle C}{4})$ = 1

Substituting the values we get

$\sqrt \frac{1 \times 4}{r^2} + \sqrt \frac{1 \times 9}{r^2} + \sqrt \frac{4 \times 9}{r^2}$ = 1

$\frac{2}{r}$ + $\frac{3}{r}$ + $\frac{6}{r}$ = 1 $\Rightarrow$ $r = \boxed {11}$