Tangent Circles
Two circles, each with radii 900, are tangent to each other and they are both tangent to a line. Find the radius of the circle which is tangent to both circles and also the line.
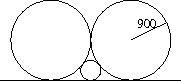
The answer is 225.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
wonderful ..how did u draw the figure?
Log in to reply
Use p a i n t and upload it at this link .
Geogebra?
same solution here :3
My triangle was different, because I used the bigger and not the smaller. So, It's wrong
Log in to reply
You got it right and somebody else used a different method. This does imply that the other method is wrong. Please be more kind before commenting.
Same method here! :)
did it exactly the same way..
Very good solution !
good solution
wonderful
4got this hehh
nice figure it makes it easy to understand......
fantastic figure
Protip: Use difference of squares:
9 0 0 2 = ( 9 0 0 + R ) 2 − ( 9 0 0 − R ) 2 = ( 9 0 0 + R + 9 0 0 − R ) ( 9 0 0 + R − 9 0 0 + R ) = ( 1 8 0 0 ) ( 2 R ) ⟹ R = 2 2 5 .
unfortunately i put 15 (took the square root for some reason), so I gave up :(
mindblowing
thanks
I used a relation between the tangents i.e tangent=√ r*R
good
It can be solved easily by using 1/sq. root(c)=1/sq. root(a) +1/sq. root(b)
Let larger radius be R = 9 0 0 and smaller radius be r .
Draw a line parallel to given line through center of smaller circle.
Draw a perpendicular on it from center of a larger circle.
We get a right angled triangle with sides, R , R − r and R + r
By Pythagoras theorem, R 2 = ( R + r ) 2 − ( R − r ) 2 ⇒ R = 4 ⋅ r ⇒ r = R / 4 = 9 0 0 / 4 = 2 2 5
Why we cannot use R + r in both situation?
Log in to reply
observe that, by symmetry, center of smaller circle will lie on vertical line through Point of contact of larger circles.
Thats why the triangle i am referring to will have base as R and not R + r.
Apply to Ford Circle's formula for 2 tangent circles and 1 circle between 2 circles same as fig. Ford Circle
R m i d d l e 1 = R l e f t 1 + R r i g h t 1
R l e f t , r i g h t = 9 0 0 ;
R m i d d l e 1 = 9 0 0 1 + 9 0 0 1
R m i d d l e 1 = 3 0 2 = 1 5 1
Therefore: R m i d d l e = 1 5 2 = 2 2 5
seeing it for the first time.
Thanks for the link of Ford Circle. :)
that simple.. omg..
Draw a line from the center of the right big circle (radius = 900) to the center of the small circle, then draw a line perfectly horizontal until you are right under the center of the big circle, and then go back to the center of the big circle. This is a right triangle. Let's call the radius of small circle r .
What you can see is that the horizontal side is, in fact, 9 0 0 , the vertical side is 9 0 0 − r , and the hypotenuse is 9 0 0 + r . Now that we have that, all we must do is use Pythagorean theorem ( a 2 + b 2 = c 2 ) and solve for r , the radius of the small circle.
9 0 0 2 + ( 9 0 0 − r ) 2 = ( 9 0 0 + r ) 2
9 0 0 2 + ( 9 0 0 2 − 1 8 0 0 r + r 2 ) = 9 0 0 2 + 1 8 0 0 r + r 2
9 0 0 2 = 3 6 0 0 r
3 6 0 0 9 0 0 2 = r = 2 2 5
We see, from the Pythagorean Theorem, that
( 9 0 0 ) 2 + ( 9 0 0 − r ) 2 = ( 9 0 0 + r ) 2 ⟹ r = 2 2 5 .
r = raio da circunferência menor --------> r = ?
R = raio da circunferência maior ---------> R = 900
- Resolvendo esta equação:
( R + r ) 2 = ( R ) 2 + ( R − r ) 2 --------> ( 9 0 0 + r ) 2 = ( 9 0 0 ) 2 + ( 9 0 0 − r ) 2
r = 2 2 5
x 2^2+(r 1-r 2)^2=(r 1+r_2)^2
for x_2, giving
x 2=2sqrt(r 1r_2).
x 3^2+(r 1-r 3)^2 = (r 1+r_3)^2
(x 3-x 2)^2+(r 2-r 3)^2 = (r 2+r 3)^2
for x 3 and r 3, giving
x 3 = (2r 1sqrt(r 2))/(sqrt(r 1)+sqrt(r_2))
r 3 = (r 1r 2)/((sqrt(r 1)+sqrt(r_2))^2).
The latter equation can be written in the form
1/(sqrt(r 3))=1/(sqrt(r 1))+1/(sqrt(r_2)).
It all depend upon the theorem of tangent to circle, two tangent meeting at a point have equal length. So we can solve by applying this principle, we will get r=900/4=225
In this specific formation : two touching congruent circles, with a smaller circle in between, that is tangent to both larger circles; the radius (r) of the smaller circle is always 1/4 of the radius (R) of the larger circles.
r = R/4 = 900/4 = 225
From seeing the figure. The radius should be 1/4 of the 1st circle.
diameter of small circle=900/2=450,
radii of small circle=450/2=225
Let k 1 be curvature of two big circles & k 2 be curvature of small circle. Here we can apply special case of descartes' theorem where one mutually tangent circle is a line & two circles are equal.
k 2 = k 1 + k 1 + 2 k 1 k 1
k 2 = 9 0 0 1 + 9 0 0 1 + 2 9 0 0 1 ⋅ 9 0 0 1
k 2 = 9 0 0 2 + 9 0 0 2
k 2 = 2 2 5 1
hence, the radius = c u r v a t u r e 1 = 225 .
If you join the middle of the circle to the middle of the smaller circle of radius r, and then draw a triangle with one side being 900 and other from center of smaller circle to the point where 2 bigger circles touch, you will get a right angled triangle with sides 900, 900 - r and hypotenuse of 900 + r. Applying pythagorean theorem, you get (900+r)^2 = (900-r)^2 + 900^2. Solving this for r you get r = 225
2*(diameter of small circle)=(radius of bigger circle)/2
use ford circle law 1/[sqrt{r}]radius of small circle=1/\sqrt{R}RADIUS OF LEFT CIRCLE+1/\sqrt{R'}RADIUS OF RIGHT CIRCLE
1/[sqrt{r}]=1/\sqrt{900}+1/\sqrt{900} 1/[sqrt{r}]=1/30+1/30
i think now you can do ur self.
Let the radius of the small circle = r ---> (900+r)^2 = 900^2 + (900-r)^2 solving ---> r = 225
in the following fig. name first and second circle wid centre as p and q.
centre of the smaller circle be O.
join O to q that would be r +R(radius of the smaller circle + radius of the bigger circle) likewise form a right angle triangle of sides, R+r,R, R-r inside the circle of centre q
so by Pythagoras theorem, r+R^{2} = R-r^{2} + R^{2} ......by this equation u will get r=225
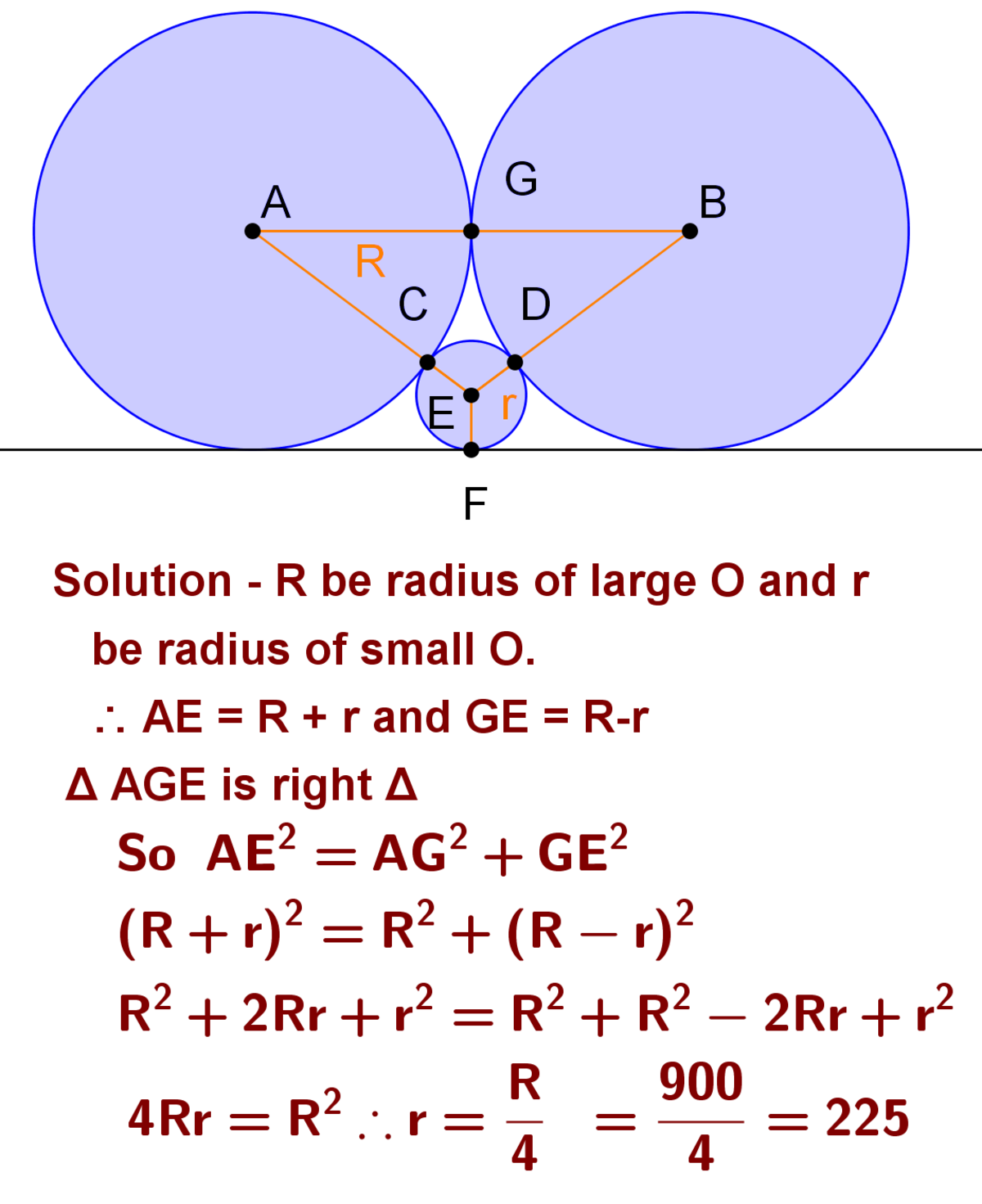
Let the radius of smaller circle be R image
9
0
0
2
+
(
9
0
0
−
R
)
2
=
(
9
0
0
+
R
)
2
⟹
R
=
2
2
5
image
9
0
0
2
+
(
9
0
0
−
R
)
2
=
(
9
0
0
+
R
)
2
⟹
R
=
2
2
5