Tangent Circles

Let $R=8cm,\,r,\,h\,$ be the radius of the major circles, the radius of the minor one, and the height of the equilater triangle with circumcenter in the center of the minor circle and vertices in the centers of the major circles; it can be observed that that the radius of the circle in which the equilater triangle is inscribed is, by the fact that the cicumcenter of a equilater triangle coincides with its centrod (see e.g equilater triangle ) :

$R_c=R+r={\frac 2 3}h;$

by Pythagorean theorem applied to right angled triangle of cathetes $R,\,h,\,$ and hypothenuse $2R,\,$ we get:

$h=\sqrt{({2R)}^2-R^2}=R\sqrt 3;$

$R+r={\frac 2 3}R\sqrt 3={\frac 2 {\sqrt 3}}R;$

$r=(\frac 2 {\sqrt 3}-1)R\approx\boxed{1.238cm}$

Let R be the circumradius of the equilateral triangle formed by joining the centres of the three circles & r be the radius of inner circle. Now $R\cos 30=8\Rightarrow R=16/√3= 9.23$ Now on joinoing the centre of inner circle & that of any big circle, it is clear that, $R=8+r$ $\Rightarrow r=9.23-8=\boxed{1.23}$

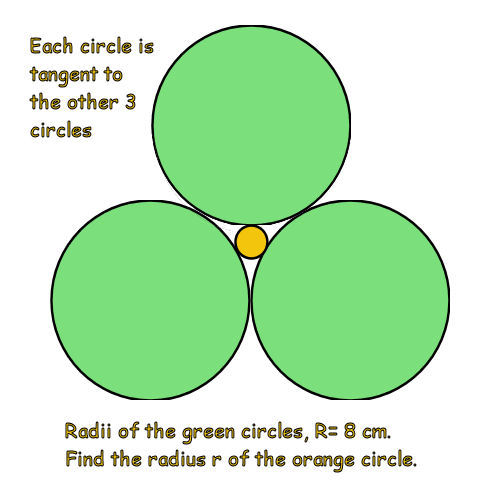
• Connect the centres of the green circles to form an equilateral triangle with each side 16 cm.
• The centre of the orange circle (O) is also the centre of the equilateral triangle formed.
• Join the centre of the orange circle with the centre of the green circles and form 3 isocles triangles. With one side of 16 cm and two of (8+r) cm.
• Since the three triangles are similar, the angle of the three triangles can be separated by 360÷3 that is 120°.
• We can pick any triangle and apply the cosine rule.

c^2 = a^2 + b^2 -2ab(cos120)

c= 16 cm
a= b = (8+r) cm

I used Trig to solve this. A triangle formed by the midpoint of the 3 big circles is an equilateral triangle forming 3 - 60degree angles. Drawing a line from one of these points to the midpoint of the small circle forms a 30 degree angle.

This sets up the following triangle: Hypotenuse is from Midpoint of the large circle to the midpoint of the small circle and has a length $l = 8 + r$ where r is the radius of the small circle ( the solution we are looking for).

The length of the adjacent side is from mid point of the large circle to the midpoint on the line between this point and the midpoint of the adjacent large circle and its length is $l = 8$ , the radius of the large circle.

Although we could calculate it, we do not need to know the length of the opposite leg of this triangle for our solution so we ignore that.

The angle is 30 degrees and the cosine of 30 degrees is 0.866 Trig tells us that the ratio of the adjacent side to the hypotenuse is the cosine of the angle so that sets up the following equation:

$\frac {8}{8+r} = cos(30)$

so

$8 = 0.866 * (8+r)$

solving for r returns our solution which is

$1.2376043072 = 1.238$ (solution to 3 decimal places).

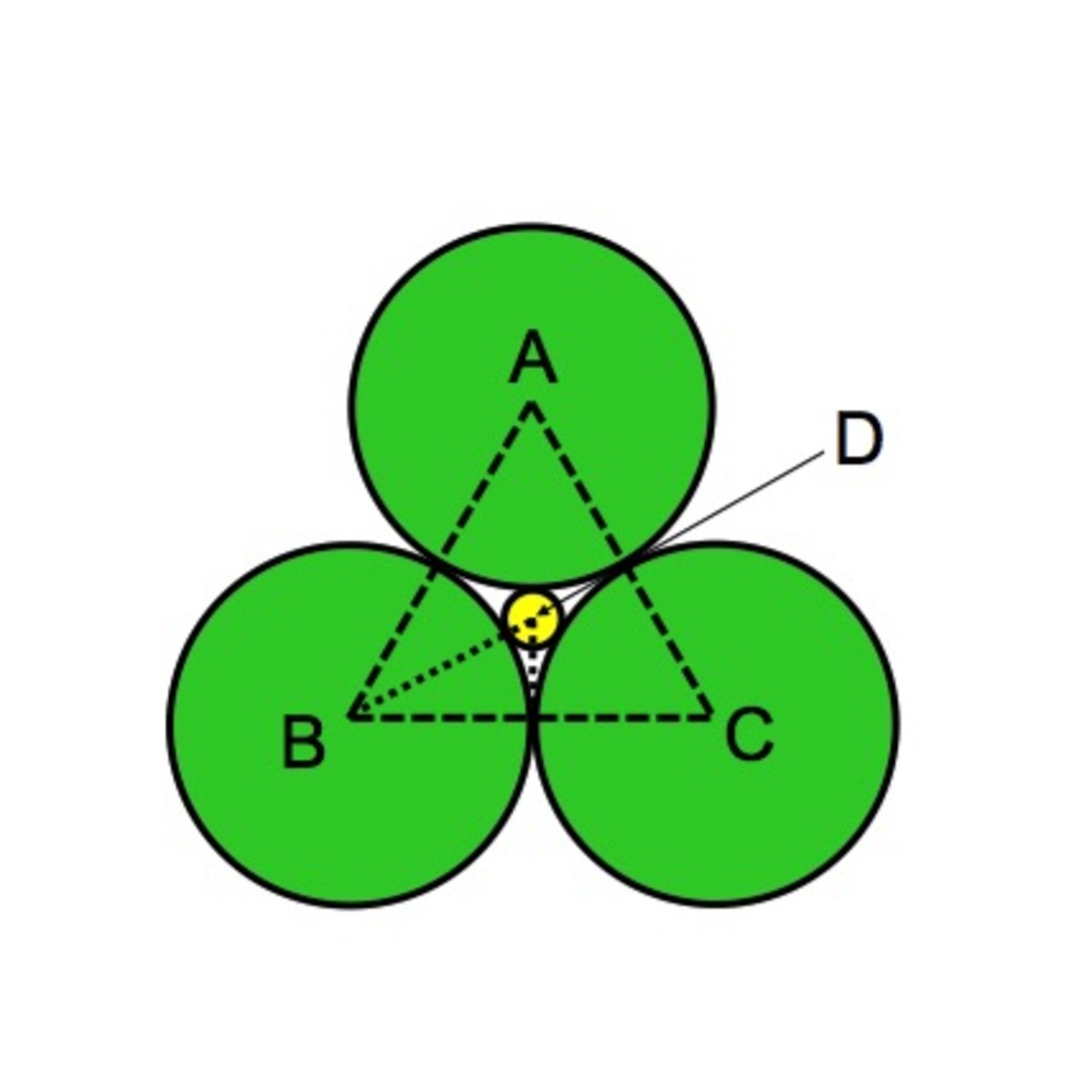
If two circles are tangent, their centers and the point of tangency are collinear. Therefore, the segments joining each circle's center to the center of the other two circles (AB, BC, and CA) will create a triangle. Because the radii of all green circles are 8, the triangles will have congruent sides, making it equilateral (and equiangular).

For an equilateral triangle, the incenter, orthocenter, and centroid are the same point, which is represented by point D (see figure above). Therefore, angle DBC is 30 degrees and the perpendicular segment drawn from D to BC bisects BC into two congruent (8 cm) radii.

Call the point of tangency between circles B and C point E (not pictured above). Triangle DBE is a 30-60-90 triangle (using information above and triangle sum theorem). Now I will use trig to finish the problem. The cosine of DBE (which is 30 degrees) would equal the length of BE (which is 8) divided by BD (which is 8 cm of the green circle's radius plus the radius of the yellow circle).

cos(30) = 8/(8 + x)
cos(30) = sqrt(3)/2

sqrt(3)/2 = 8/(8 + x)
now cross multiply

sqrt(3)*(x + 8) = 16
divide by sqrt(3)

x + 8 = 16/sqrt(3)
subtract 8

x = 16/sqrt(3) - 8
which is approximately 1.238

let A,B and C are the centers of green circles

D is center of yellow circle triangle ABC is equal and each angle = 60 Deg draw triangle ABD use sin law AB/sin(ADB) = AD/sin(ABD) where AB=16cm ,angle ABD=30 Deg and angle ADB=120Deg calculate AD = 9.238 radius of yellow circle = AD-8

If the three outer circles have radii of a, b & c then the radius of the inner circle is given by abc/(ab+bc+ca+2√(abc(a+b+c)) If instead you are interested in an outer circle which touches the three circles then it's radius = - abc/(ab+bc+c-2√(abc(a+b+c)). Of course, in this case, a=b=c=r which can be calculated as 8/(3+2√3) ~1.2376

A solution without trigonometry.........(sorry for the shaky diagram.)

Here let O be the center of the orange circle.

Let r=x.......for the sake of algebra!

PQ=QR=PR=16 cm...(8+8)

In triangle OQR,

QR=16 cm, OQ=OR=8+x

Also triangles POQ ,QOR,POR are congruent.

Therefore, A(PQR)= $3[\sqrt{(16+x)(x)(8)(8)}]$ ...................by Heron's Formula

Also A(PQR)= $\sqrt{3}/4 *16^2$ ........area of an equilateral triangle

By solving both and equating we get: $3x^2 + 48x - 64 = 0$

The roots of this quadratic equation are $16/3 * \sqrt{3} - 8$ and $- 8 - 16/3 * \sqrt{3}$

But we want positive solution ..

Therefore x = r = $\boxed{1.238}$ (approx)

Imagine a large triangle with vertices at the centers of the green circles, then use the cosine rule, or similar to find the distance from the center of a green triangle to the center of the orange triangle, now take the radius of a green circle from this and you're done ;-)

(8/cos30)-8=1.238

let the radius of green circles be R and that of yellow circle be r . Join the centres of the green circles. now a n equilateraltriangle is formed with side 16cm. the centre of the yellow circle is the centroid of the equilateral triangle. let us name the triangle ABC and the centroid of yellow circle O . join AD where D is the mdpoint of BC and this AD passes through O. now find AD using pythagoras theorem , AD^2 = AB^2 - BD^2. we get AD=8 x sqrt(3) = 13.856

now we know that O divides AD in the ratio 2:1. so AO = 2/3 x AD.= 2/3 x 13.856 = 9.28352

now AO is ( R+r.) R+r = 9.28352 r = 9.28352 - 8 = 1.28352 .

Well my solution is a bit round the clock so try to keep up: Form an equilateral triangle with the centers of the three circles. Find the height of the given triangle by 30-60-90 triangle formula i.e. Height=8* Sqrt(3)= 13.856

Height -8= 5.854 which will give the height from the top of the yellow circle to the bottom of the equilateral triangle.

At this point we only need to minus the height below the mid-point to reveal the actual radius. Which can be quite tricky. Just form another 30-60-90 triangle by 1 -connecting center of a green circle with that of the yellow circle, 2- Center of yellow with the intersection of two green circle & 3- Center of green circle with the intersection of the previous point of intersection of two circles. This gives you required height= 4.6188. All you got to do is subtract this with 5.854. Which gives the Radius of Yellow Circle = 5.856406461-4.618802154= 1.237604

.Hope this is helpful. If you find the answer difficult to understand just draw the triangles i mentioned above.

let the distance between the centers of one of the green circle (considerleft circle with center 'o') and yellow (o1 as center )one be 'd' i.e ,radius of green circle 'r' , radius of yellow circle be 'x'.

you will find : d=r+x. let p be the meeting point of left and right green circles.

the angle oo1 and op is 30degrees(since op is the angular bisector at o which forms an equilateral triangle with other centers ( green cirlces) therefore angel" o" being part of the circle is 60 degrees... being the bisector angle o1op=30 degrees )

from triangle oo1p:

d sin(30)= op=r=8

there fore d=8/sin(30)=9.238(approx) but d=r+ x => x=d-r => x= 9.238-8=1.238

therfore x= 1.238cm or the radius of the yellow circle is= 1.238

by sin rule: 16 x sin(30)/sin(120) - 8 = 1.238

if radius of big circle is R & small circle is r.to joining big circles R it becames eqibriliiam triangle.so angle is 60 .so half angle is 30 .so by using trigo cos30`=R/R+r.put values,you get ans

Centres of the green circles make an equilateral triangle with side L = 16cm

The distance of the centroid, which is also the position of the centre of the yellow circle, from any of the vertex is given by L/√3

Now : L/√3 = R(green) + R(yellow)

R(yellow) = (16/√3) - 8 = 9.2376 - 8 = 1.2376