Some more Tangent Circles.
Given three circles which share the same tangent and touch each other as shown in the figure,
If the radius of the larger Orange Circle is 9 units and that of the smaller Green circle is 4 units.
What is the radius (correct to two decimal places) of the white circle which lies in between both the circles and also shares the same tangent ?
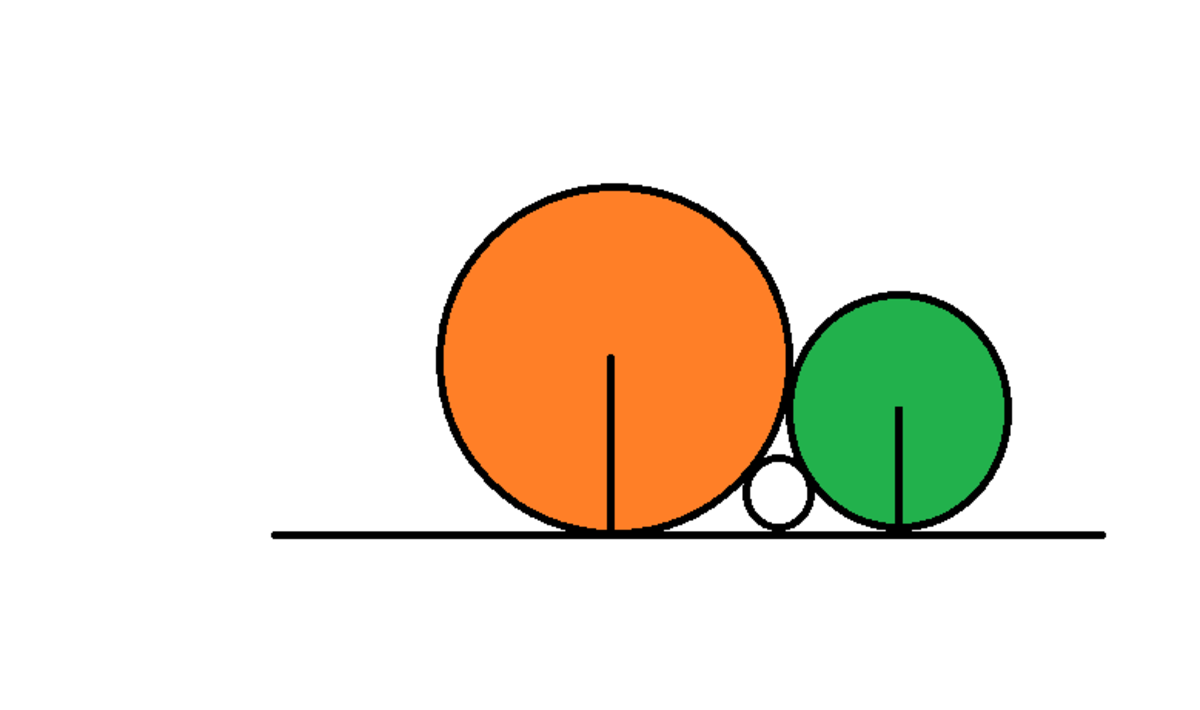
The answer is 1.44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Suppose a is the radius of the Orange Circle and b is the radius of the Green circle, Let us assume that c is the radius of the white circle in between...
It can be shown using Pythagoras theorem that
sqrt(ab) = sqrt(bc) + sqrt(ac)
Dividing by sqrt(abc) throughout,
1/sqrt(c) = 1/sqrt(a) + 1/sqrt(b)
Substituting the value of a and b from the problem, we arrive at c = 1.44 units.