Tangent Cuts

Geometry Level 4

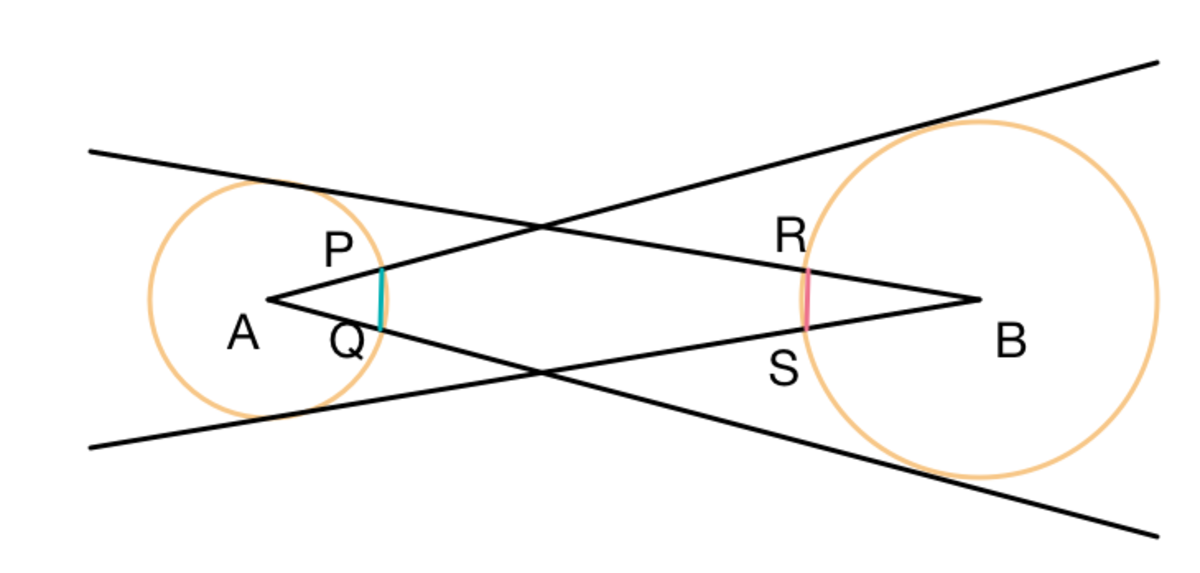
Circle $\Gamma_1$ centered at $A$ has a smaller radius than circle $\Gamma_2$ centered at $B$ .

From $A$ , the tangents to $\Gamma_2$ intersect $\Gamma_1$ at $P$ and $Q$ .
From $B$ , the tangents to $\Gamma_1$ intersect $\Gamma_2$ at $R$ and $S$ .

Which line segment is longer, $PQ$ or $RS$ ?

The answer depends on the relative sizes

RS

PQ

They have the same length.

1 solution

Marta Reece
May 13, 2017

Let’s calculate $PM=\frac12 PQ$ as a function of $r_1$ and $r_2$ .

Triangles $ANB$ and $AMP$ are similar, therefore $\frac{r_2}{AB}=\frac{PM}{r_1}$

This can be written as $PM=\frac{r_1r_2}{AB}$ where the distance $AB$ is constant.

This means that $PM$ will not change if the roles of the two radii are exchanged.

Since $PQ=2 PM$ , it too will remain the same if $r_1$ is replaced with $r_2$ and vice versa.

But exchanging the radii makes $RS$ out of $PQ$ , therefore $PQ=RS$

Tangent Cuts

1 solution

0 pending reports