Tangent paraboloid to the three coordinate planes
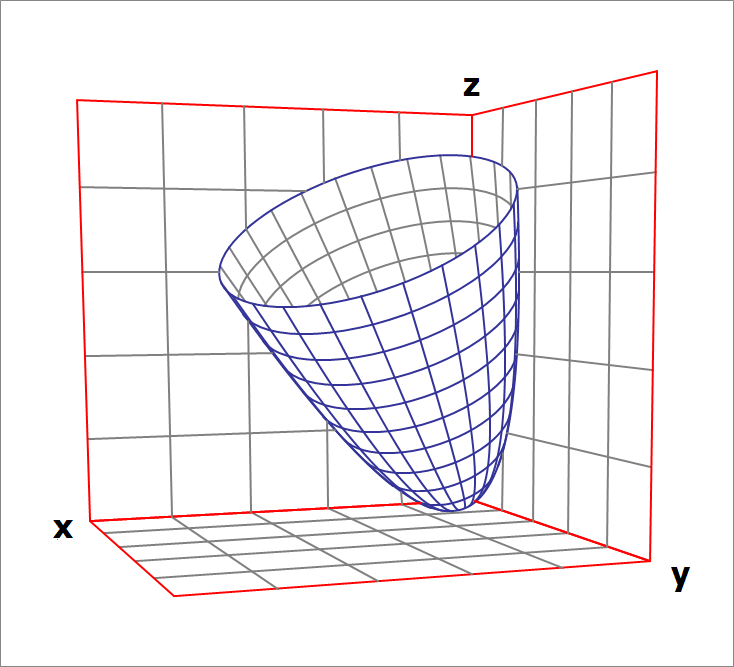
The paraboloid is tilted and shifted such that its axis of symmetry is along the unit vector , with , and such that it becomes tangent to the three coordinate planes. If , and are the tangency points with the , and planes, respectively, then find .
The answer is 36.789.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The parametric equation of the paraboloid z = a x 2 + b y 2 is
p ( r , t ) = ( x , y , z ) = ( a r cos t , b r sin t , r 2 )
After rotation and translation, the parametric equation is modified to,
p ( r , t ) = r v + R ( a r cos t , b r sin t , r 2 )
where r v = ( r 1 , r 2 , r 3 ) is the coordinate vector of the vertex, and the 3 × 3 rotation matrix R can be specified as follows, R = [ u 1 , u 2 , u 3 ] , where u 3 (the third column of R ) is the unit vector of the symmetry axis of the rotated paraboloid, thus u 3 = ( sin θ cos ϕ , sin θ sin ϕ , cos θ ) . The first and second columns of R point in the new directions of the x-axis and the y-axis, respectively. In the case where a = b , as in this problem, their orientation does not matter, and they can therefore, be any two mutually orthogonal vectors which are also orthogonal to u 3 .
At the tangency point with the x y plane, the partial derivatives of p with respect to r and t lie in the x y plane, so that their z-coordinate is zero. Differentiating,
p r = ∂ r ∂ p = R ( a cos t , b sin t , 2 r )
p t = ∂ t ∂ p = R ( − a r sin t , b r cos t , 0 )
if k = [ 0 , 0 , 1 ] T , then k T p t = 0 , and since r = 0 , this equation can be solved, in a straightforward manner for t .
Define v = [ v 1 , v 2 , v 3 ] T = R T k , then
v T ( − a r sin t , b r cos t , 0 ) = 0
so that,
− a v 1 sin t + b v 2 cos t = 0
For which the solution is,
cos t = − a v 1 2 + b v 2 2 a v 1 , and sin t = − a v 1 2 + b v 2 2 b v 2
The reason for the negative signs will become apparent shortly. Now, we also have that v T p r = 0 , from which,
− a v 1 2 + b v 2 2 + 2 v 3 r = 0
And hence, r = 2 v 3 1 a v 1 2 + b v 2 2
Note that v 3 > 0 because v 3 = cos θ , hence this last equation will lead to a positive value of r .
Now that we have found r and t , we utilize the fact that z = 0 at the tangency point, to write,
k T p = 0 = r 3 + v T ( a r cos t , b r sin t , r 2 )
Plugging in the values of r , cos t and sin t , we get,
0 = r 3 + 2 v 3 1 a v 1 2 + b v 2 2 ( − a v 1 2 + b v 2 2 + 2 1 a v 1 2 + b v 2 2 )
So that, after simplification,
r 3 = 4 v 3 1 ( a v 1 2 + b v 2 2 )
This formula can be applied to obtain r 2 and r 1 , but with the vector v modified to R T j and R T i , respectively, where j = [ 0 , 1 , 0 ] T and i = [ 1 , 0 , 0 ] T .
This completes the specification of the three tangency points.
Another approach is to use the algebraic equation of the paraboloid instead of the parametric vector equation described above.
The algebraic equation is given by,
( r − r v ) T R D R T ( r − r v ) + c T R T ( r − r v ) = 0 ( 1 )
where D = diag { a , b , 0 } and c T = [ 0 , 0 , − 1 ]
The gradient (which is normal to the surface of the paraboloid) is given by
∇ = 2 R D R T ( r − r v ) + R c ( 2 )
At the tangency point r 1 with the x y plane, this gradient points in the negative direction of k , the unit vector along the positive z -axis. Hence,
2 R D R T ( r 1 − r v ) + R c = − α k ( 3 . 1 )
where α > 0 .
Similarly, the gradient equation at r 2 , the tangent point with the x z plane is,
2 R D R T ( r 2 − r v ) + R c = − β j ( 3 . 2 )
and, for r 3 , the tangency point with the y z plane, we can write,
2 R D R T ( r 3 − r v ) + R c = − γ i ( 3 . 3 )
where β > 0 and γ > 0 .
It turns out that we can determine the multipliers α , β , γ very easily, as follows.
Premultiplying both sides of equation (3.1) by R T , we obtain
2 D R T ( r 1 − r v ) + c = − α R T k ( 4 )
Since the third row of matrix D is zero, the third row of equation (4) reads,
− 1 = − α k T R T k ( 5 )
Hence α can be determined, namely, α = R 3 3 1 . A similar argument leads to
β = R 2 3 1 and γ = R 1 3 1 .
Now consider equation (4) again, we need to solve for r 1 − r v . Since the columns of matrix R form a basis for R 3 ,
we can write,
( r 1 − r v ) = R p 1 ( 6 )
for some unique vector p 1 = ( p x , p y , p z ) . Plugging (6) into (4), yields
2 D p 1 + c = − α R T k ( 7 )
The third row of (7) reads 0 + ( − 1 ) = − 1 , while the first two rows read,
2 a p x = − α i T R T k ( 7 . 1 )
2 b p y = − α j T R T k ( 7 . 2 )
So that,
p x = ( 2 a 1 ) ( − α i T R T k ) = − 2 1 a R 3 3 R 3 1 ( 7 . 3 )
p y = ( 2 b 1 ) ( − α j T R T k ) = − 2 1 b R 3 3 R 3 2 ( 7 . 4 )
The third element of vector p 1 which is p z is undetermined yet. To determine it, we substitute for
( r 1 − r v ) from (6) into the paraboloid equation, which is equation (1). This leads to,
( R p 1 ) T R D R T ( R p 1 ) + c T R T ( R p 1 ) = 0 ( 8 )
And since R is a rotation matrix, it follows that R T R = I , hence, equation (8) becomes,
p 1 T D p 1 + c T p 1 = 0 ( 9 )
Expanding the left hand side, we obtain,
a p x 2 + b p y 2 − p z = 0
Since p x and p y are known, this determines p z , namely
p z = 4 1 ( a R 3 3 2 R 3 1 2 + b R 3 3 2 R 3 2 2 ) ( 1 0 )
Back to equation (6), and taking the z coordinate of the vector ( r 1 − r v ) , we obtain,
0 − r 3 = k T R p 1 = p x R 3 1 + p y R 3 2 + p z R 3 3
So that the z coordinate of the vertex is given by,
r 3 = − p x R 3 1 − p y R 3 2 − p z R 3 3 = 4 R 3 3 1 ( a R 3 1 2 + b R 3 2 2 ) ( 1 1 )
And this is the same formula we obtained in the previous approach. In a similar fashion, we can arrive at,
r 2 = 4 R 2 3 1 ( a R 2 1 2 + b R 2 2 2 ) ( 1 2 )
r 1 = 4 R 1 3 1 ( a R 1 1 2 + b R 1 2 2 ) ( 1 3 )
Now that the vertex is fully specified, as well the vector p 1 , we can write,
r 1 = r v + R p 1 ( 1 4 )
Similarly,
r 2 = r v + R p 2 ( 1 5 )
r 3 = r v + R p 3 ( 1 6 )