Tangent sphere to a cube
A sphere of radius 3 2 is tangent to the edges A B , A D , A A 1 , and the face diagonal C D 1 of the cube A B C D A 1 B 1 C 1 D 1 .
The volume of the cube can be written as a + b c , where a , b are integers and c is a square-free positive integer. What is the value of a + b + c ?
Details and assumptions
The order of the vertices in the cube is shown on the picture below.
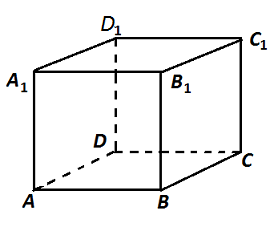
Face diagonal simply means the diagonal of a face. It is technically not an edge of the cube, which is why we denoted C D 1 separately.
The answer is 252.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Which point is K?
It's almost evident (and easy to prove) that the center O of any sphere that touches AB,AD,AA1 lies on the diagonal AC1. X - the orthogonal projection of O in the plane CDD1 lies on DC1. Let M be the midpoint of CD1. As DC1 is perp. to CM, and OX is perp. to CM this means that CM is perp. to any line of the plane OXM, and in particular to the line OM (in my coutry we call this the theorem of 3 perpendiculars). This shows that the sphere touches CD1 at M. From OM=R we obtain a^2-8a+6=0 (where a is the side lenght of the cube). Obviously a>3 and we get a=4+srqt(10). The volume is 184+58xsqrt(10). a+b+c=252.
Choose A as the origin of the Cartesian corodinate system, and AB, AD, and AA1 as x. y, z axes. Let the side length of the cube be 2s. Because of symmetry, let the center of sphere be O=(x,x,x).
r=3sqrt(2) = xsqrt(2), hence x=3. The sphere is tangent to CD1 at the midpoint M of CD1. M=(s, 2s, s). r=OM. Namely r^2 = OM ^2. i.e. 18= (s-3)^2+(s-3)^2+(2s-3)^2.
Solve the above quadratic equation: 2s^2-8s+3=0, s=2+sqrt(10)/2.
Hence AB=2s=4+sqrt(10). Volume V=(2s)^3=184+58sqrt(10)
Suppose the center of the sphere is the point O . Because O is at the same distance from the edges A B , A D , and A A 1 , its projection onto these edges is at the same distance from A . If this projection of O onto A B is at the distance x from A , then the distance from O to the plane A B C D is also x . Therefore, from the Pythagorean theorem, the radius of the sphere is x 2 , thus x = 3 .
Suppose the length of A B is y . Then the distance from O to the plane C C 1 D 1 D is y − 3 . Suppose the projection of O to that plane is E . Clearly, E must lie on the face diagonal D C 1 , at the distance 3 2 from the point D . Its distance from the line C D 1 is then 2 y − 3 2 = 2 y − 6 . By the Pythagorean Theorem, the distance from O to C D 1 is ( y − 3 ) 2 + ( 2 y − 6 ) 2 = 2 3 y 2 − 2 4 y + 5 4 Setting this equal to the radius of the sphere, 3 2 , we get a quadratic equation on y : 3 y 2 − 2 4 y + 1 8 = 0 , which simplifies to y 2 − 8 y + 6 = 0 . There are two roots: y = 4 − 1 0 and y = 4 + 1 0 , of which the first one is impossible, because y has to be greater than 3 for the sphere to be tangent to the edges and not their continuations.
So, the cube has side 4 + 1 0 and its volume is ( 4 + 1 0 ) 3 = 6 4 + 4 8 1 0 + 1 2 0 + 1 0 1 0 = 1 8 4 + 5 8 1 0 Therefore, the answer is 1 8 4 + 5 8 + 1 0 = 2 5 2 .
We call that AB measure is L.
Draw axes to use analytic geometry with origin at A.
AB is positive x axe, AD negative y axe and AA1 positive z axe.
So we have:
A = (0,0,0) C = (L,-L,0) D1 = (0,-L,L)
Now we must find the point 3sqrt(2) away from AB, AA1 and AD.
To do this we must make cylinders over AB, AA1 and AD with radius 3sqrt(2).
x²+y²=18, x²+z²=18 and y²+z²=18 represent those cylinders.
The solutions to this equations, this could be verified, satisfies the condition. The solution that we are looking for is (3,-3,3), because its the only one that could have the 3sqrt(2) distance from CD1. (this could be verifiable too, both verifications from Pythagoras theorem).
Now that we have the point X = (3,-3,3) we will find L using areas. To do this we must use
XC.XD1.sen(CXD1)/2 = 3sqrt(2).CD1/2
CD1 = Lsqrt(2)
to find sen(CXD1) we must use Law of cossines to find cos(CXD1) and use the Pythagorean Trigonometric Identity,
XC and XD1 could be easily found with the coordinates.
I wish I could draw diagrams, but I will explain as clearly as I can.
Let P be the center of the sphere described in the problem, its projection on A B , A D , A A 1 , A B C (plane), A 1 A B , A 1 A D be U , V , W , X , Y , Z resp. Thus by the property of tangents, U , V , W are where the sphere is tangent to A B , A D , A A 1 resp., which means A U = A V = A W . Since P is the intersection of the planes through U , V , W but parallel to planes A 1 A D , A 1 A B , A B C resp., thus A U X V W Y P Z is a cube, since the diagonal of a face of this cube is equal to P U = P V = P W = 3 2 , thus it has edge length 2 3 2 = 3 .
Let a be the edge length of A B C D A 1 B 1 C 1 D 1 . Now let's use the Pythagorean theorem to find the lengths of P D 1 and P C , thus for R T △ P C X we have P C 2 = P X 2 + C X 2 . Since X is on the diagonal A C , thus C X 2 = ( A C − A X ) 2 = ( a 2 − 3 2 ) 2 = 2 ( a − 3 ) 2 , so P C 2 = 3 2 + 2 ( a − 3 ) 2 . For P D 1 , we let the projection from P to A 1 B 1 C 1 be T , thus D 1 P 2 = P T 2 + D 1 T 2 . Easy to see that P T 2 = ( a − 3 ) 2 . Now focus on plane A 1 B 1 C 1 , let the projection from T to A 1 D 1 be S , then by the Pythagorean theorem for R T △ D 1 T S we have D 1 T 2 = T S 2 + D 1 S 2 = 3 2 + ( a − 3 ) 2 , thus D 1 P 2 = ( a − 3 ) 2 + 3 2 + ( a − 3 ) 2 = 3 2 + 2 ( a − 3 ) 2 , which is the same as P C 2 ! So P C = P D 1 .
Let the projection from P to C D 1 be K , Since △ P C D 1 is isosceles, so K is the midpoint of C D 1 , thus C K = 2 D 1 C = 2 a 2 . Now by using the Pythagorean theorem on R T △ P C K , we get P C 2 = P K 2 + C K 2 . Note that since the sphere is tangent to CD_1, so K is the point of tangency, thus P K = 3 2 and we have 3 2 + 2 ( a − 3 ) 2 = ( 3 2 ) 2 + ( a 2 / 2 ) 2 , by solving this quadratic equation we obtain a = 4 + 1 0 ( 4 − 1 0 is ignored). So the volume of A B C D A 1 B 1 C 1 D 1 is ( 4 + √ 1 0 ) 3 = 1 8 4 + 5 8 √ 1 0 , thus the answer is 1 8 4 + 5 8 + 1 0 = 2 5 2 .
Let the centre of the sphere be point O. From point O, construct O E ⊥ A B and O F ⊥ A 1 A and O G ⊥ P l a n e A 1 A D D 1 and O H ⊥ P l a n e A B C D and O I ⊥ C D 1 and O J ⊥ P l a n e C D C 1 D 1 and O L ⊥ P l a n e A 1 B 1 B A .
By symmetry, O G = O H = O L . Hence, △ O H E is isosceles right triangle. O H = E H = 2 3 2 =3. For the same reason, A E = A F = O G = G F = O H = H E = 3 and △ K J I is also isosceles and K I = K J .
Let E B = A 1 F = n . K I = 2 3 + n − 3 = 2 n − 3 . It is followed by I J = 2 2 n − 3 .
Because A B = A D , it follows that O J = E B = n . Based on I J 2 + J O 2 = O I 2 , ( 2 2 n − 3 ) 2 + n 2 = ( 3 2 ) 2
Solve the equation and n = 1 + 1 0 . Hence, the side length equals to 1 + 1 0 + 3 = 4 + 1 0 . The volume equals to ( 4 1 0 ) 3 = 1 8 4 + 5 8 1 0 The answer is 1 8 4 + 5 8 + 1 0 = 2 5 2