Tangent Trapezoid
Two circles with radius 3 and 1 2 are externally tangent to each other.
Let C D and E F be the common external tangent to both the circles with C and F on one circle and D and E on the other circle.
What is the area of the trapezoid C D E F ?
The answer is 115.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
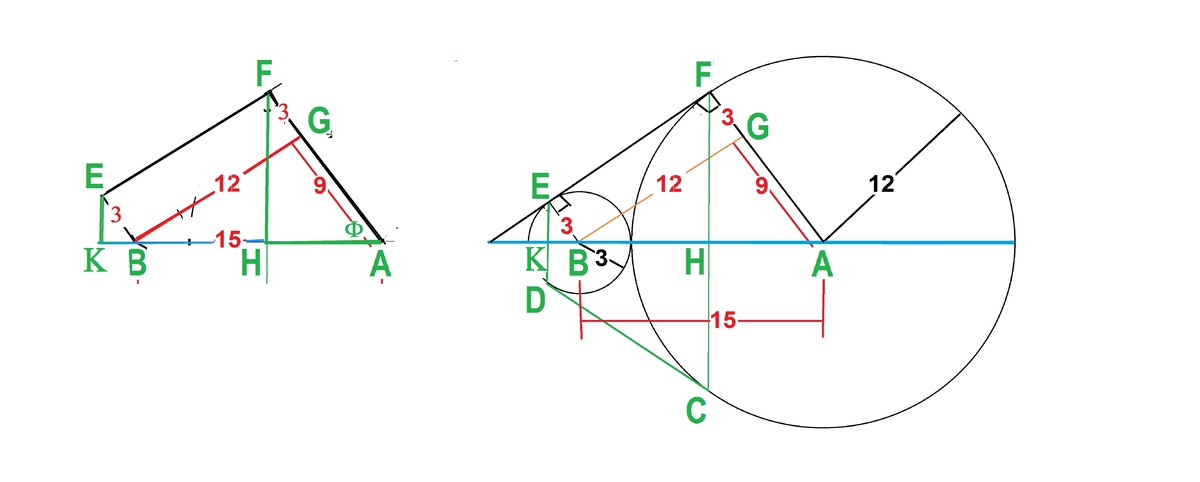
A and B are the centers of the circles. Tangent chord ED cut line of centers AB at 90 degrees at H. Tangent chord FC cut line of centers AB at 90 degrees at K.
D
r
a
w
B
G
=
a
n
d
∣
∣
E
F
.
S
o
F
G
=
E
B
a
n
d
9
0
d
e
g
r
e
e
a
t
G
a
n
d
A
G
=
1
2
−
3
=
9
.
r
t
.
∠
d
Δ
A
G
B
,
A
B
=
3
+
1
2
=
1
5
,
A
G
=
9
∴
B
G
=
1
2
.
∠
B
A
G
=
ϕ
.
S
i
n
ϕ
=
5
4
,
C
o
s
ϕ
=
5
3
.
r
t
.
∠
d
Δ
A
F
H
,
A
H
=
A
F
C
o
s
ϕ
=
1
2
∗
5
3
,
F
H
=
A
F
S
i
n
ϕ
=
1
2
∗
5
4
r
t
.
∠
d
Δ
B
E
K
,
B
K
=
E
B
C
o
s
ϕ
=
3
∗
5
3
,
E
K
=
B
E
S
i
n
ϕ
=
3
∗
5
4
A
r
e
a
t
r
a
p
e
z
i
u
m
F
E
K
H
=
2
1
(
E
K
+
F
H
)
∗
(
H
K
)
=
2
1
(
E
K
+
F
H
)
∗
(
A
B
−
A
H
+
B
K
)
=
2
1
(
3
∗
5
4
+
1
2
∗
5
4
)
(
1
5
−
1
2
∗
5
3
+
3
∗
5
3
)
=
5
7
.
6
.
∴
a
r
e
a
C
D
E
F
=
2
∗
5
7
.
6
=
1
1
5
.
2
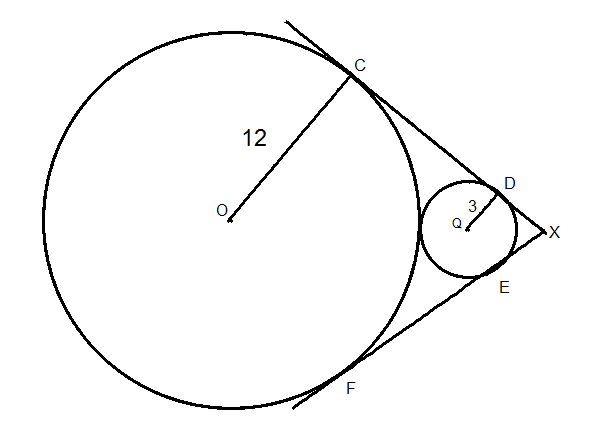
Focus on O Q E F that is rectangle trapezoid and O Q = 1 5 → 1 5 2 = ( 1 2 − 3 ) 2 + h 2 → h = 1 2 ∴ F E = C D = 1 2
Let m = D X , we have that △ O C X ∼ △ Q D X and O C ∣ ∣ D Q so m 1 2 + m = 3 1 2 → m = 4
Let h 1 height of △ Q D X since D → D E = 2 h 1 so 2 h 1 × 5 = 2 3 × 4 → h 1 = 5 1 2
Let h 2 height of △ O C X since C → C F = 2 h 2 so 2 h 2 × 2 0 = 2 1 2 × 1 6 → h 2 = 5 4 8
D E = 5 2 4
C F = 5 9 6
As trapezoid C D E F is isosceles and let h 3 its height. C D 2 = ( 2 C F − D E ) 2 + h 3 2 → h 3 = 1 2 2 − ( 7 . 2 ) 2 = 9 . 6
Area of the trapezoid C D E F = 2 ( D E + C F ) h 3 = 2 ( 5 2 4 + 5 9 6 ) ( 9 . 6 ) = 1 1 5 . 2
First i will find the generalization the problem.
Let the radius of the circles be a and b .Let [ K L M . . . X Y Z ] denote the area of polygon K L M . . . X Y Z .
Let the common internal tangent intersect C D and E F at points P and R respectively. Let Q be the intersection of A B and P R . Tangents to a circle from an external point have the same length. Therefore,
P C = P Q = P D
and
R E = R Q = R F
By symmetry, P Q = R Q . Therefore,
C D = P R = E F
Construct P S perpendicular to E F with S on E F and A G perpendicular to B E with G on B E .
Triangles P S R and A G B are similar since corresponding sides are perpendicular to each other. Therefore,
P R P S = A B A G
Since A G = E F , we have
E F 2 = A B 2 − B G 2 = ( b + a ) 2 − ( b − a ) 2 = 4 a b
and
P S = A B E F 2 = ( a + b ) 4 a b
See first
P D C P = R F E R implies
[ C D E F ] = [ P E F ] + [ R C D ] = 2 [ P E F ]
= P S . E F = ( a + b ) 8 a b a b .
So put a = 3 and b = 1 2 in the above expression to get the Area A = 1 1 5 . 2
(1/ 2)(a + b)
= (1/ 2) [2 R Sin q + 2 r Sin q]
= (R + r) [2 Sqrt (R r)/ (R + r)] = 2 Sqrt (R r)
h
= r (R - r)/ (R + r) + R + r - R (R - r)/ (R + r)
= 4 R r/ (R + r)
Area of trapezium
= (1/ 2)(a + b) h
= 8 R r Sqrt (R r)/ (R + r)
= 8 (12)(3) Sqrt (12 x 3)/ (12 + 3) = 1728/ 15 = 115.2
Note: Cos q = (R - r)/ (R + r) and hence Sin q = 2 Sqrt (R r)/ (R + r) while both circles applied the same angle in calculations.
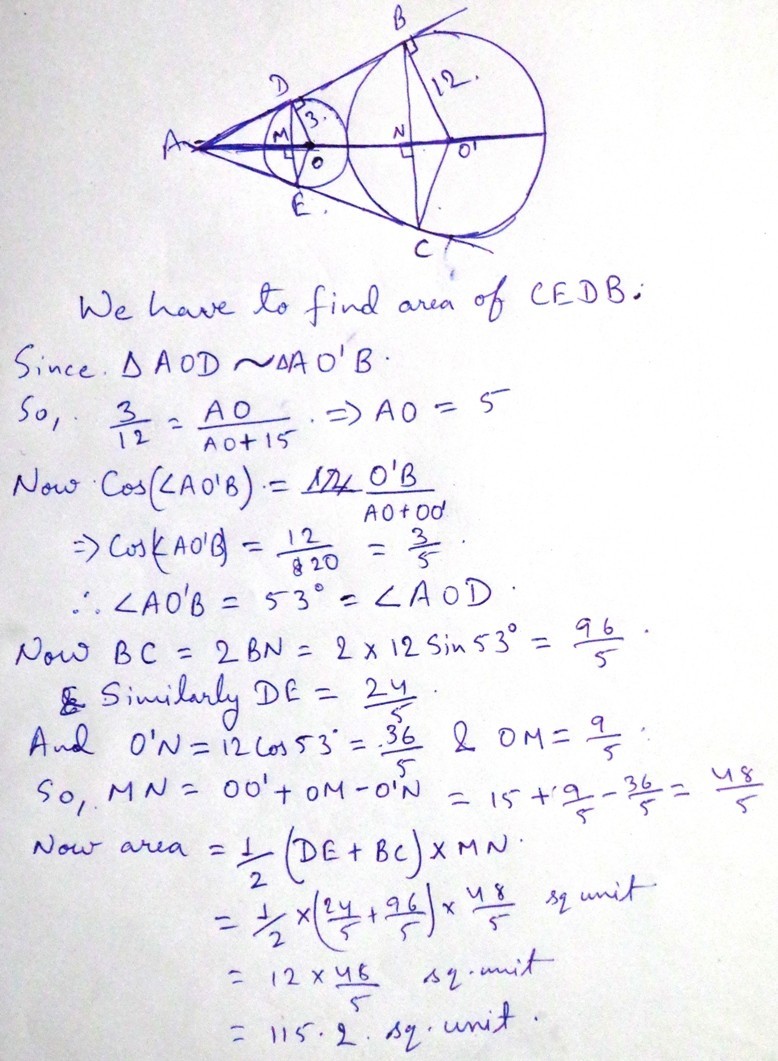 Here is the solution.
Here is the solution.