Tangentia Dance
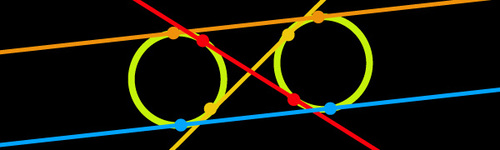 In a 2D world, the circles are organizing a
'Circle Party'
, where they sing and perform their traditional
'Tagentia Dance'
.
In a 2D world, the circles are organizing a
'Circle Party'
, where they sing and perform their traditional
'Tagentia Dance'
.
In the 'Tangentia Dance' , all the Circles arrange themselves in a circle and hold the largest possible number of different ribbons such that the ribbons are tangents to both of the Circles holding them.
If 2 0 Circles are performing this year, how many ribbons are required for the 'Tangentia Dance' ?
Details and assumptions :
- The question talks about the maximum number of tangents possible between all the circles.
- Every ribbon is connecting only 2 Circles.
The answer is 760.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Nice! Neat solution.
Between each two circles, there are a total of four possible tangents, as shown in the diagram.
There are ( 2 2 0 ) = 1 9 0 ways to choose a pair of circles.
Thus 1 9 0 × 4 = 7 6 0 is the answer.
Yep ! I think the figure actually gave all the hints :P
The number of ribbons between two circles is 4;the no of two circle pair are 20C_2 .
Hmm. Quite the short answer there. I guess the image gave away all the hints
Well...lets start with 2 circles... we need 4 ribbons(as seen thru the diag) When we add 1 more circle....we need 4+(4 2) ribbons When there are 4 circles...we need 4+(4 2)+(4*3) circles like that for 20 circles we will require 4(1+2+3+.....20).. calculating the sum of this series, we get the answer to be 760...CHEERS!!!
Nice. This problem can be done by other easier methods too. Refer other solutions too.
Total number of pairs of circles = C(20, 2) = 190.
There is a maximum of 4 possible tangents between 2 circles when the circles are not intersecting, not touching/kissing and not inside one another.
Number of ribbons = 190 * 4 = 760
The first circle could make 19 other pairs and the second one could make 18 other pairs .... etc so we can form a sequence
( 1 9 , 1 8 , 1 7 , 1 6 , 1 5 , 1 4 , 1 3 . . . . . . . . . . . 3 , 2 , 1 )
and we calculate the sum of them
2 1 9 × ( 1 + 1 9 ) = 1 9 0 and we multiply it by 4 because every pair of circles make 4 ribbons 1 9 0 × 4 = 7 6 0
every pair of circle have max 4 tangents and 20C2 =190 is the number of different pair of circle among 20. So 4*190=760 is the answer.
There are 4 ribbons required for each pair of circles: 2 external and 2 internal tangents. Furthermore, there are ( 2 2 0 ) such pairs of circles, for a total of 4 ⋅ ( 2 2 0 ) = 7 6 0 ways.
its oral ques.... for 2 we need 4 for 3 we need 8+4 for 4 we need 12+8+4 follows an arithemetic progression.... for 20 we need 76+72+68+....+4=760
Each circle may only share 4 ribbons with any other circle, which is an obvious factor. Knowing this, we now just need to know with how many circles we need to share. The first circle of the 20, shares with the other 19, the next, already having shared with the first, shares with the other 18, the next shares with the remaining 17 and so on, meaning we have a total of 190 "interactions" between circles. As each of these interactions consists of 4 ribbons, we calculate the answer as 190*4, giving the solutions of 760 ribbons.
take any 2 circles at a time and b/w 2 circles 4 tangents (2 direct n 2 indirect) are possible. so answer will be (nC2) *4
where, n= no. of circles; C stands for combination!!!!
Every circle shares 4 ribbons with each of the other circles. Circle #1 shares 4*19 ribbons i total. Circle #2 shares 4*18 ribbons with the remaining 18 circles (not counting with #1) Circle #3 shares 4*17 ribbons and so on. We then get the following sum of the total amount of ribbons: 4 ∗ 1 9 + 4 ∗ 1 8 + 4 ∗ 1 7 + . . . + 4 ∗ 1 = 4 ( 1 9 + 1 8 + 1 7 + . . . + 1 ) = 4 ( 2 0 ∗ 9 + 1 0 ) = 4 ∗ 1 9 0 = 7 6 0
Notice that each pair of circles can form 4 ribbons between them. There are a total of ( 2 2 0 ) = 1 9 0 different pairs amongst the 2 0 circles, so the total number of ribbons will be ( 2 2 0 ) ⋅ 4 = 1 9 0 ⋅ 4 = 7 6 0