Tangential Essentials II
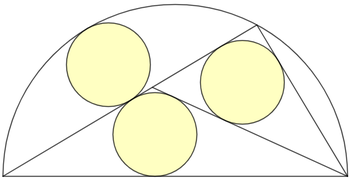
In the semicircle of radius , the point selected on the circumference forms two identical incircles each inscribed in their own triangles, where one of them is an incircle of a right triangle. There exists the unique positive radius, such that the centrally positioned circle, sharing one point of tangency with the circumference of the circle and also one point of tangency with the largest triangle, has the same radius as two incircles.
If the radius is , input as your answer.
Try this sister problem first before you attempt this one.
The answer is 243477.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Label the diagram as follows:
By symmetry on the top left circle, D F is the perpendicular bisector of A C , so △ A E F ∼ △ A C B by AA similarity, and since E F = D F − D E = 1 − 2 R , that makes C B = E F ⋅ A E A C = ( 1 − 2 R ) ⋅ 2 = 2 − 4 R .
By the Pythagorean Theorem on △ A C B , A C = A B 2 − C B 2 = 2 2 + ( 2 − 4 R ) 2 = 4 R − R 2 .
Let k = G C . By the Pythagorean Theorem on △ G C B , G B = G C 2 + C B 2 = k 2 + ( 2 − 4 R ) 2
Also from right △ G C B , R = 2 1 ( G C + C B − G B ) = 2 1 ( k + 2 − 4 R − k 2 + ( 2 − 4 R ) 2 ) , which solves to k = 3 R − 1 R ( 5 R − 2 ) .
From △ A G B , R = P △ A G B 2 A △ A G B = A G + G B + A B A G ⋅ C B = ( 4 R − R 2 − k ) + k 2 + ( 2 − 4 R ) 2 + 2 ( 4 R − R 2 − k ) ( 2 − 4 R ) .
Substituting k = 3 R − 1 R ( 5 R − 2 ) into R = ( 4 R − R 2 − k ) + k 2 + ( 2 − 4 R ) 2 + 2 ( 4 R − R 2 − k ) ( 2 − 4 R ) and solving numerically gives R ≈ 0 . 2 4 3 4 7 7 2 , and ⌊ 1 0 6 R ⌋ = 2 4 3 4 7 7 .