Tangential right trapezoid
A circle is inscribed in a right trapezoid with base lengths 22 and 35.
What is the area of this trapezoid?
The answer is 770.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Same solution, great job Sir!
I understand that a quadrilateral with just one pair of sides parallel is a trapezium, and something ending "-oid" is a 3-dimensional solid. .Or are things different on the other (Trump-infested) side of the pond?
Log in to reply
The suffix -oid means "resembling" or "in the form of." That's why the 3D analog of a 2D shape sometimes does this (ellipse, ellipsoid) but other -oid shapes are 2D (epicycloid)
My guess is that trapezium referred to a specific real object and some people began using the same word for the shape and some used the suffix -oid.
@Patrick Benham - You clearly need your brains beaten in until you wise up, because you made an assh*le, ignorant statement about the U.S. President. And, you, hypocritical piece of garbage, are allowing your lands to be infested with uncontrolled Muslim "refugee" lawlessness, go-to zones, etc. Take your political statements and anti-U.S. indoctrination comments and get off the board.
That's how I solved it too.
Log in to reply
1234567890
Log in to reply
Runa --- what is the significance of 1234567890 here ? :-)
Clever, short and simple!
Very impressed couldn’t figure .Frugal (or area) of a cone like pi unknown... I thought if had an angle or a slanted bottom? Would there be a constant? definite solution.
Is this just a coincidence that 22 x 35 = 770 ?
Log in to reply
Algebraically, it's definitely not a coincidence. If we let a = 2 2 and b = 3 5 , then the Pythagorean theorem on C H D becomes ( a − b ) 2 + 4 x 2 = ( ( a + b ) − 2 x ) 2 . Expanding the RHS and simplifying yields ( a − b ) 2 − ( a + b ) 2 = − 4 ( a + b ) x . So x = a + b a b .
This also implies that the area of any right trapezoid in which a circle can be drawn tangent to all four sides is the product of the two bases, which is an interesting formula.
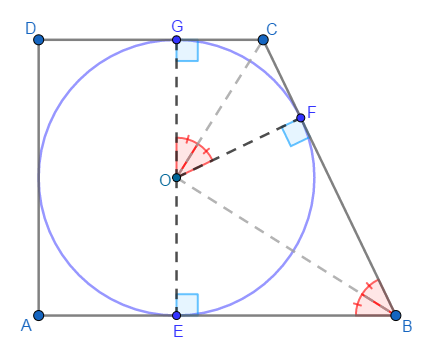 Let
r
be the radius of the circle and
E
,
F
and
G
tangential points, so:
∠
O
E
B
=
∠
O
G
C
=
9
0
°
. Since the center of a circle inscribed in an angle lies on its bisector:
Let
r
be the radius of the circle and
E
,
F
and
G
tangential points, so:
∠
O
E
B
=
∠
O
G
C
=
9
0
°
. Since the center of a circle inscribed in an angle lies on its bisector:
∠ E B O = ∠ F B O = 2 1 ∠ E B F and ∠ F C O = ∠ G C O = 2 1 ∠ F C G .
Also, since ∠ E B F + ∠ F C G = 1 8 0 ° : ∠ C O G = 9 0 ° − ∠ G C O = 9 0 ° − 2 1 ∠ F C G = 2 1 8 0 ° − ∠ F C G = 2 1 ∠ E B F = ∠ E B O
So, triangles △ E B O and △ G O C are similar, which means: O E C G = B E O G ⇒ r 2 2 − r = 3 5 − r r .
Solving this equation gives us r = 5 7 7 7 0
Area of the trapezoid is: 2 A B + C D ∗ A D = 2 2 2 + 3 5 2 r = 2 ∗ 5 7 5 7 ∗ 2 ∗ 7 7 0 = 7 7 0
Is this just a coincidence that 22 x 35 = 770 ?
Log in to reply
Wow, no.
O E C G = B E O G ⇒ r C D − r = A B − r r
so
A B ⋅ C D = ( A B + C D ) r
but at the same time area is
2 A B + C D 2 r = ( A B + C D ) r
so area is A B ⋅ C D
Let the sloping line on the right hand side have length L and the diameter of the circle be D.
Pitot's theorem states that each pair of opposite sides of a quadrilateral with an in-circle sum to the same total! So
D + L = 5 7 … ( 1 )
An easy application of Pythagoras gives
D 2 + 1 3 2 = L 2 ⟹ ( L − D ) ( L + D ) = 1 6 9
Substitute from (1) to get
L − D = 5 7 1 6 9
Subtract this from (1) and divide by 2 to get
D = 5 7 1 5 4 0
Which gives the area of the trapezium as
2 1 ( 2 2 + 3 5 ) 5 7 1 5 4 0 = 7 7 0
Nice solution!
1234567890
Let R be the radius of the circle. Let the lengths of top and bottom bases be a ± b ; in this case, a = 2 8 2 1 and b = − 6 2 1 . Then the area of the trapezoid is A = 2 a R .
Choose a coordinate system with the origin O at the center of the circle. The two vertices on the right then have coordinates V ± = ( a ± b , ± R ) . The point of tangency between these vertices has coordinates T ( a − R + b x , R x ) for some − 1 < x < + 1 . The segment O T satisfies two conditions:
-
its length is R , i.e. ( a − R + b x ) 2 + ( R x ) 2 = R 2 ;
-
it is perpendicular to the side V − V + , i.e. the vectors ( a − R + b x , R x ) and ( b , R ) are perpendicular: ( a − R + b x ) b + R 2 x = 0 .
We multiply the second equation by x and subtract it from the first to obtain ( a − R ) ( a − R + b x ) = R 2 ; substituting this again into the second equation, we get ( a − R + b x ) ( b + ( a − R ) x ) = 0 . This implies x = − b / ( a − R ) , and our third equation becomes R 2 = ( a − R ) 2 − b 2 ∴ 2 a R = a 2 − b 2 ∴ R = 2 a ( a + b ) ( a − b ) . Finally, the area is A = 2 a R = ( a + b ) ( a − b ) = 2 2 ⋅ 3 5 = 7 7 0 .
Astounding. :-)
For any right trapezoid with an inscribed circle that touches all four sides, the area is equal to the product of the two widths of the trapezoid.
22 x 35 = 770
Do you know of any proofs of that statement of yours?
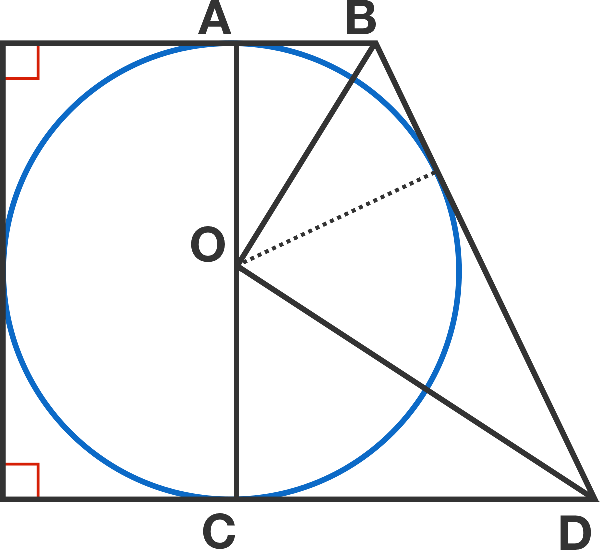 By comparing angles, we can see that right-triangle
△
B
A
O
is the same shape as
△
O
C
D
By comparing angles, we can see that right-triangle
△
B
A
O
is the same shape as
△
O
C
D
We know that O C and A O both equal the radius r , and by extension, C D = 3 5 − r and B A = 2 2 − r .
As the two triangles are proportionate, the ratio B A : A O is the same as O C : C D . From this, we can work out the radius:
r 2 2 − r = 3 5 − r r
r 2 = ( 2 2 − r ) ( 3 5 − r )
r 2 = 7 7 0 − 5 7 r + r 2
0 = 7 7 0 − 5 7 r
5 7 r = 7 7 0
r = 5 7 7 7 0
And so the area is 2 1 × ( 2 × 5 7 7 7 0 ) × ( 3 5 + 2 2 ) = 7 7 0
This may have been completely coincidental, but I just took the two given lengths and multiplied them together. So 22(35) = 770
It's not coincidental at all.
If you take Jeremy Galvagni's solution and substitute with variables 'a' and 'b' for the lengths 22 and 35 you will find the area is indeed 'ab'.
The area of a convex poligon can be found by S=p.r , where p represents half the perimeter and r is the radius of the inscribed circle. Moreover, the Area of any trapezoid is also A = ( b + B) .h/2, where B is the 'bigger' base, b the smaller one and h the hight, which in this case equals to twice the radius.
So : p.r = (22+35) .(2r)/2
p= 57
If we close a rectangle triangle by connecting the furthest right point of the smaller base to it's projection on the bigger base, we are gonna have the triangle with sides 13, h and √(13²+h²).
With that, we have:
Perimeter = 22+ 35 + h + √(13²+h²) = 2p
57 + h + √(13²+h²) = 2. 57 =>
√(13²+h²) = 57-h =>
169 + h²= 57² - 114h + h² =>
114h = 3249-169 =>
h = 1540/57
By using this result above, we have: S=(22+35) .h/2 => S= (57 . 1540)/ (2. 57) => S= 1540/2 => S= 770
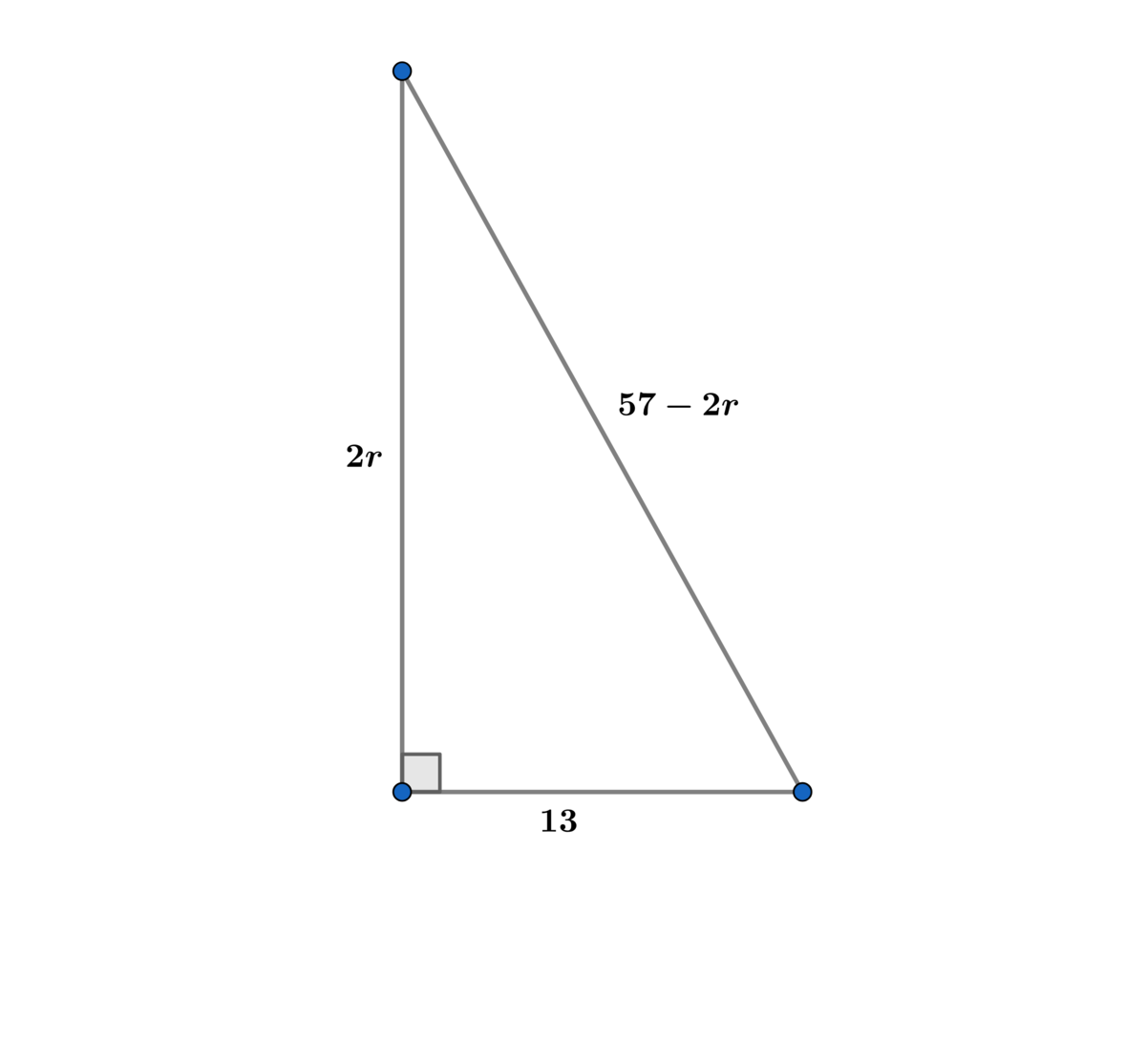
( 5 7 − 2 r ) 2 = ( 2 r ) 2 + 1 6 9 ⟹ 3 2 4 9 − 2 2 8 r = 1 6 9 ⟹ r = 5 7 7 7 0 ⟹
Tha area of the trapezoid A e = 5 7 r = 7 7 0 .
Let us consider the radius of the circle to r. Let the parallel sides of the trapezium be a and b.
We can use Harmonic mean (HM) to find the radius. HM = r = ab/a+b
Area of the trapezium being 1/2 * h * (a+b) where we can equate h = 2r
Solving by substituting the value of a we get Really of eight tangential trapezoid to be the product of the parallel sides (i.e) ab
Hence A = 22*35 = 770
 Above is someone else's work for solving for the radius of an inscribed circle for a right trapezoid/trapezium.
Above is someone else's work for solving for the radius of an inscribed circle for a right trapezoid/trapezium.
Our radius in this case is (22*35)/57
Next: The formula for the area of a trapezoid is 0.5*(b 1+b 2)*h.
b_1 = 22
b_2 = 35
h = 2*r = 2*(22*35)/57
Therefore: A = 0.5*(57)*2*(22*35)/57
Since 0.5*2 and 57/57 are both 1, our area is just 22*35 = 770.
It can be proved that the area equals the product of the lengths of the parallel sides. I wonder if there exists a visual proof...

Let x be the radius. Then E C = 2 2 − x , F D = 3 5 − x , C H = 1 3 , H D = 2 x .
By congruent triangles, C G = 2 2 − x and G D = 3 5 − x , so C D = 5 7 − 2 x .
By right triangle C H D we have 1 3 2 + ( 2 x ) 2 = ( 5 7 − 2 x ) 2
Solving gives x = 5 7 7 7 0
And so the area sought is 2 1 ⋅ ( 2 x ) ⋅ ( 2 2 + 3 5 ) = 7 7 0