Tangential Trapezoid

Geometry Level 3

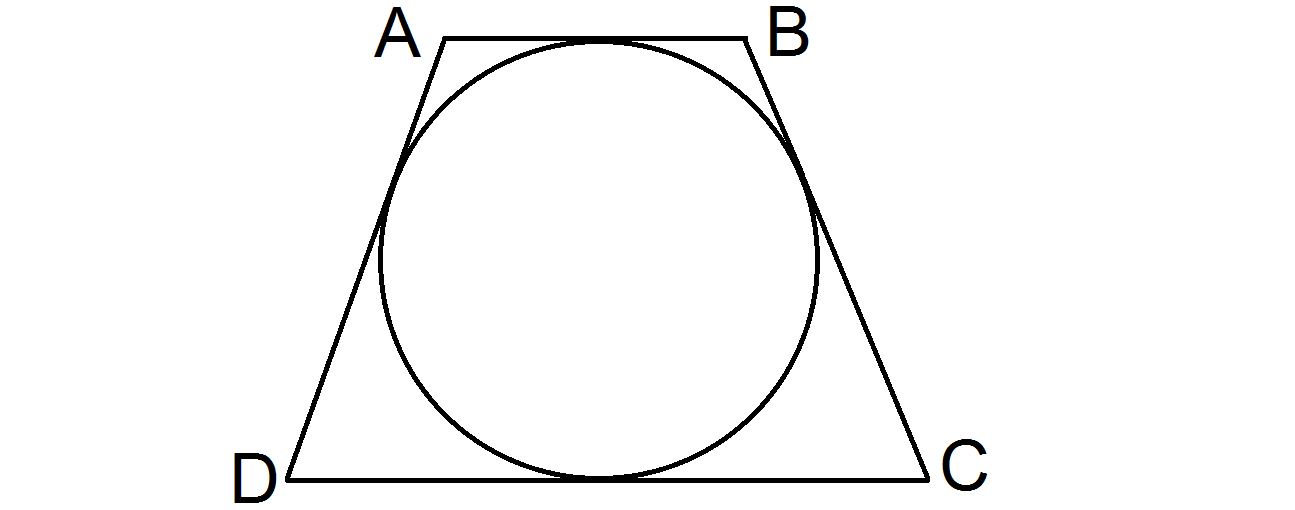
A B C D ABCD is a tangential isosceles trapezoid, touching the circle as shown above.

If the perimeter of the trapezoid is 52, and the circle's radius and all trapezoid's sides have lengths in whole integers, what is the area of the trapezoid?


The answer is 156.

View wiki
Worranat Pakornrat by Worranat Pakornrat , 36, Thailand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

According to Pitot's Theorem , for a tangential quadrilateral, A B + C D = A C + B D AB + CD = AC + BD .

Since the perimeter is 52 52 , then 52 = ( A B + C D ) + ( A C + B D ) = 2 ( A B + C D ) 52 = (AB + CD) + (AC + BD) = 2(AB + CD) . A B + C D = 26 AB + CD = 26 .

All we need to know now is the height of the trapezoid, which is also the diameter of the circle because both radii from the touching points at A B AB and C D CD make the right angles with these parallel lines.

Now suppose x x be the distance from touching point to either A A or B B and y y the distance from that to C C or D D and h h be the height of the trapezoid.

Now when we draw a perpendicular line down from point A A to C D CD :

By Pythagorean Theorem, h 2 + ( y − x ) 2 = ( y + x ) 2 h^2 + (y-x)^2 = (y+x)^2 .

h 2 = 4 x y h^2 =4xy

h = 2 x y h = 2\sqrt{xy}

Since the radius is the whole integer, and x + y = A D = B C = 13 x+y = AD = BC = 13 , both x x and y y are perfect squares. Hence, x + y = 4 + 9 x + y = 4 + 9 .

Then h = 2 4 × 9 = 12 h = 2\sqrt{4\times 9} = 12 .

As a result, the area of the trapezoid = ( A B + C D 2 ) h = 13 × 12 = 156 (\dfrac{AB + CD}{2})h = 13\times 12 = \boxed{156}

9 Helpful 0 Interesting 0 Brilliant 2 Confused

The fact that xy is a perfect square does not imply that both x and y are perfect squares. (That's not even true if we constrain x and y to be integers, which we don't.) Nor does the fact that x+y=13 imply that both x and y are integers. The only things we are told to be integers are the perimeter of the trapezoid and the radius of the circle.
Seems to me that we can let x be any value in the range from 0 to 6.5 such that x*(13-x) is a perfect square. The range of the function f(x) = x(13-x) on this interval is from 0 to 42.25 (achieved with x=6.5). Seems like there are six different possible answers here. Just find the six different values of x yielding f(x)=1, f(x)=4, f(x)=9, f(x)=16,f(x)=25, and f(x)=36. As x gets smaller and smaller these trapezoids will get flatter and flatter, looking like extremely wide, flat triangles. The top edge will be much shorter than the bottom edge, and the tangent points along the sides will be closer and closer to the top. Yes, it's very hard to visualize if f(x)=1, but f(x)=25 should yield a relatively sane looking isosceles trapezoid, with x = 0.5(13-sqrt(69)) and y =0.5(13+sqrt(69)).

Richard Desper - 3 years, 11 months ago

Log in to reply

These trapezoids have area 26n for n=1,2,3,4,5,6.

Richard Desper - 3 years, 11 months ago

OK, I've edited the problem. Thanks.

Worranat Pakornrat - 3 years, 11 months ago

In this isosceles Trapezoid, let the Tangents to the circle from A and B be m, and from D and C be n.
So AB=2m, DC=2n, ... AD=BC=m+n. ... and let the circle have a radius of r.
So the perimeter =4(m+n)=52, and m+n=13=AD and height h= 2r, r and integer.
So AD hypotenuse and h the leg are part of a Pythagorean triple 5-12-13.
2r is not 5(r is an integer), so 2r=12.
Area required=1/2 (AB+CD) h=1/2 26 12=156. By the way a=4 and b=9 because of isosceles Trapezoid.


2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...