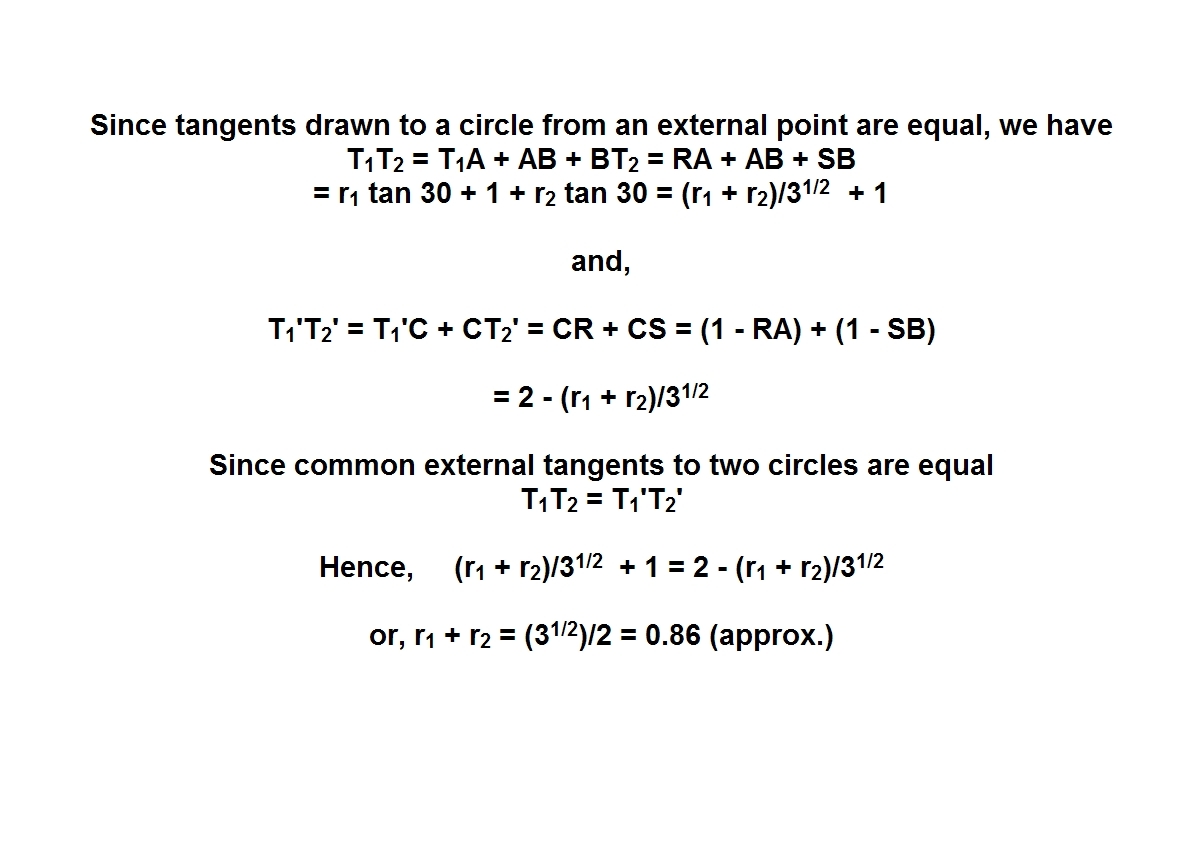Tangential Twist

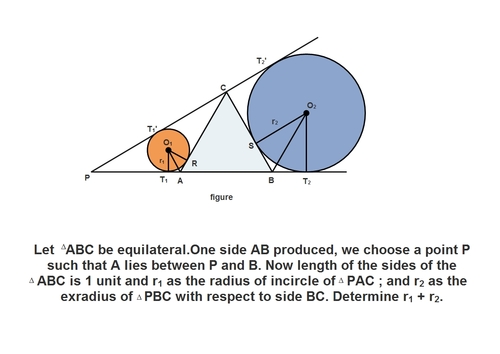
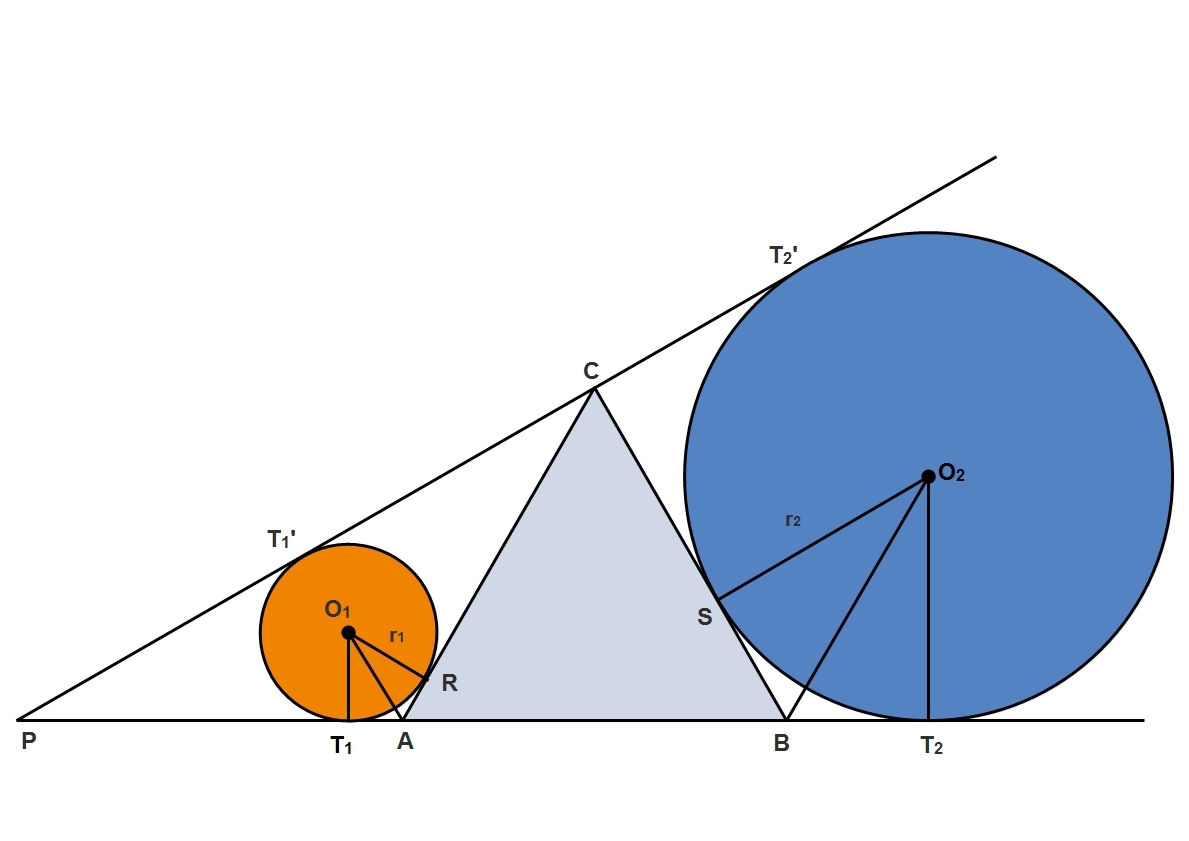
Join AO1. Drop a perpendicular from C to AB to meet at H. This is the altitude of the equilateral triangle ABC

Now consider the Triangle AT'1C .

As we know Angle CAP = 120 degrees, Angle ACT' = 60 ( As O1 is incenter) So , Angle ACT' = 30 degress.

Therefore the triangel APC is isosceles with AC =1 and AP =1. Applying law of sines, the length of PC = Sqrt(3)

The Semi-perimeter "S" of Triangle APC = (2+sqrt(3))/2

Area = S R1 (Semi perimeter multiplied with Radius of incircle) Also the area of triangle APC = 0.5 (base PA) (Height of Equilateral triange) => S R1 = 0.5 1 Sqrt(3)/2 On Solving we get R1 = 0.232 --------------------- (1)

Now consider the angle BCT'2 . The Angle is 90 Degress, suggesting that the quadrilateral CSO2T'2 is a square with side of length R2,

Therefore CS = R2 and SB = 1 - R2

Also, the Angle T'2O2T2 is 150 degrees ( Since Angle P is 30 Degrees)

suggesting the Angle SO2T2 will be 60 Degrees.

Therefore the Angle SO2B will be 30 Degrees and the triangles SO2B and HCB are similar

=> O2S / SB = CH / HB => (R2)/(1-R2) = ( Sqrt(3)/2 ) / (1/2)

On solving R2 = 0.633 ------------------------------ (2)

Therefore R1+R2 = 0.232 + 0.633 = 0.865

"Angle ACT' = 60 ( As O1 is incenter) So , Angle ACT' = 30 degress."
Please explain. There is some typo?

$O_1T_1'=r_1.\\ In~\Delta s~T_1'PO_1~and~T_1PO_1,\\ O_1T_1' =O_1T_1, ~~~~ T_1' P = T_1 P~~equal~tangent~length,~~~~O_1P~common.\\ \angle~T_1'O_1T_1=150~~~so~\angle~T_1'PT_1=30,~~\implies~ACT_1'=30.\\ \implies~PA = AC=1. \\ In~\Delta~PAC, Using~Sin~Law, ~~PC=Sin120*AC/Sin30 =\sqrt3.\\ As~ per~ normal~ formulii, \\ Area~\Delta~PAC=.5*1*1*Sin120=\dfrac{\sqrt3} 4.\\ Area~\Delta~PBC=.5*1*1*Sin120+\dfrac{\sqrt3} 4*1^2=\dfrac{\sqrt3} 2.\\ S_1=.5*(1+1+\sqrt3). \\ S_2=.5*(2+1+\sqrt3).\\ \therefore~ r_1+r_2=\dfrac {\frac{\sqrt3} 4}{.5*(2+\sqrt3)} + \dfrac {\frac{\sqrt3} 2}{.5*(3+\sqrt3)-1} .\\ =0.86625.$