Tangents

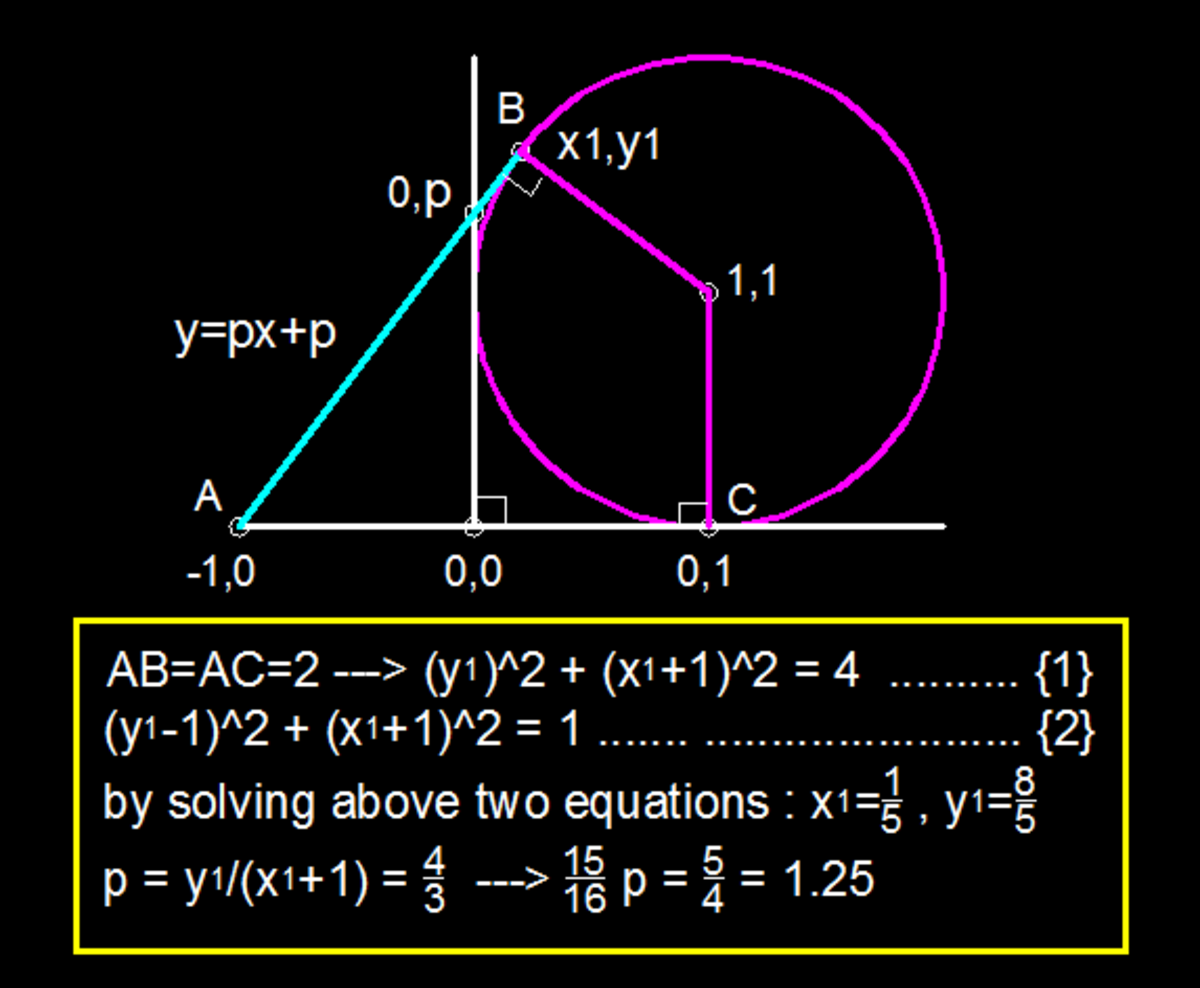
Since the circle is tangent to the axes, it has radius 1 an equation $(x-1)^2+(y-1)^2=1$ . Let $P=\dfrac{1}{k}$ . The line has equation $y=\dfrac{x+1}{k}$ . This gives $x-1=ky-2$ . We have $(x-1)^2+(y-1)^2=(ky-2)^2+(y-1)^2=y^2(k^2+1)-y(4k+2)+5=1$ .

We know that the polynomial $y^2(k^2+1)-y(4k+2)+4=0$ has real roots, therefore its discriminant is greater than or equal to zero. Since the line is tangent to the circle, we look for the greatest possible value of slope $P=\dfrac{1}{k}$ $\begin{aligned}(-(4k+2))^2-4(k^2+1)(4)\geq 0\\16k-12\geq 0\\ \dfrac{4}{3} \geq \dfrac{1}{k}=P\end{aligned}$

Hence, our answer is $\dfrac{15P}{16}=\boxed{1.25}$ .

Interesting Fact: This problem can share a similar solution to this one.