Tangents and Normals!
Let .
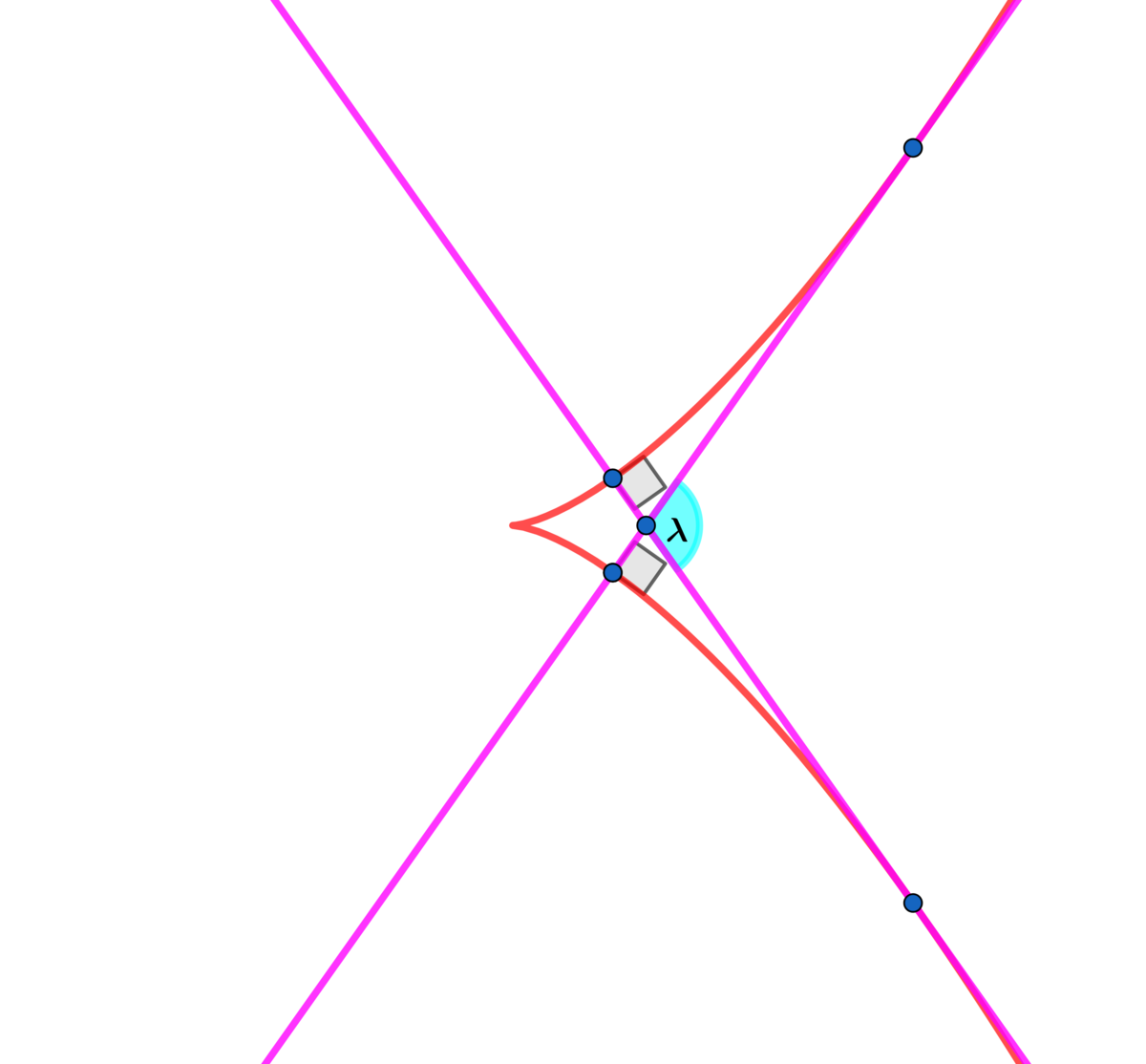
There are two lines which are both tangent and normal to the above curve.
Find the angle (in degrees) made between the two lines above.
Express the result to five decimal places.
The answer is 109.47122.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let x ( t ) = a t 2 + b , y ( t ) = b t 3 + a ⟹ d x d y ∣ ( t = t 1 ) = 2 a 3 b t 1 ⟹
the tangent line to the curve at ( x ( t 1 ) , y ( t 1 ) ) is: y − ( b t 1 3 + a ) = 2 a 3 b t 1 ( x − ( a t 1 2 + b ) )
Let the line be normal to the curve at ( x ( t 2 ) , y ( t 2 ) ) ⟹
b ( t 2 − t 1 ) ( t 2 2 + t 1 t 2 + t 1 2 ) = 2 3 b t 1 ( t 2 − t 1 ) ( t 2 + t 1 )
⟹ ( t 2 − t 1 ) ( 2 t 2 2 − t 1 t 2 − t 1 2 ) = 0 and t 1 = t 2 ⟹ t 2 = − 2 t 1
Since the tangent is also normal to the curve at ( x ( t 2 ) , y ( t 2 ) ) ⟹ 4 a 2 9 b 2 t 1 t 2 = − 1
⟹ 8 a 2 9 b 2 t 1 2 = 1 ⟹ t 1 = ± 3 b 2 2 a ⟹ the two slopes are ± 2 .
tan ( θ ) = 2 ⟹ θ = arctan ( 2 ) ≈ 5 4 . 7 3 5 6 1 ⟹ λ = 2 θ ≈ 1 0 9 . 4 7 1 2 2 .