Tangents and the Radius!
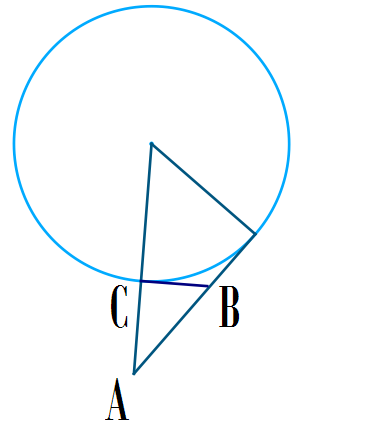 The diagrams shows a circle with radius
r
with a straight line tangent to the circle, the straight line passes through the point
A
and
B
. Given that
C
is on the point of
C
. And the distances
A
C
=
4
,
B
C
=
3
,
A
B
=
5
. Find the radius of the circle.
The diagrams shows a circle with radius
r
with a straight line tangent to the circle, the straight line passes through the point
A
and
B
. Given that
C
is on the point of
C
. And the distances
A
C
=
4
,
B
C
=
3
,
A
B
=
5
. Find the radius of the circle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
its little coplicated you can solve it by similarity and mid point theorem
simple geometry and a bit of common sense can do XD
similar property of triangles would do the trick very well!
Even though that angle is given as 37 degrees,without that information also,the problem can be solved.We can use the properties of similar triangles and that the lengths of the tangents to a circle from an external point are equal.
we can do this in a very simple way (tangent)²=secant*(secant-2r) thus 64=4(4+2r) hence r=6
How did you conclude that the line (which has a segment of specified width 5) is a tangent to the circle ? I don't think that's clear from the diagram, but I agree it makes sense to assume it since we would otherwise lack sufficient constraints to solve the problem.
Using similarity of triangles, we get: r/3 = (r + 4)/5 ==> r = 6.
The two triangles are similar. hence r/(r+4)=3/5 => r=6
Bodhayan theorem is better to use
For those who don't know , Bodhayan Theorem = Pythagorean theorem..
I used Pythagoras Identity to solve it, and also used the fact that the lengths of two tangents on a same circle from the same point are same. In the bigger triangle, ( 4 + r ) 2 = ( 5 + 3 ) 2 + r 2 Simplifying, r = 6 .
I too used this method.
using simmetry from small and large triangle, we get :
3 r = 5 r + 4
5 r = 3 r + 1 2
2 r = 1 2
r = 6
i solved it in an entirely different way. ie, by solving the equation (5+x)^2=(4+2r)4 provided that the value of x=3, we get the value for x as 3 because length of two tangents intersecting outside the circle are equal.
the formula applied here is If a secant and a tangent of a circle are drawn from a point outside the circle, then the product of the lengths of the secant and its external segment equals the square of the length of the tangent segment.
A nice way to look at the problem.
No sine needed, based on power of a point to a circle (not sure how it is translated).
-
Take the right point of the 5 against the circle. Therefore the upper tangent is 5+3(also three)
-
Based on power of the point with the angle next to it we can say that 8 8=4 (4+2r) We get a simple equation where r = 6.
QED
We can apply the use of simple trigonometry here. We should first know that tangent to a circle is perpendicular to the radius of the circle at the point of contact of the circle and the tangent. Then, by observing the right angled triangle outside the circle having sides 3 , 4 , 5 and the citcle, we get two equations ----
5 3 = sin 3 7 ∘ .....(i) and r + 4 r = sin 3 7 ∘ ........(ii)
From equations (i) and (ii) ------
r + 4 r = 5 3
⟹ 5 r = 3 r + 1 2 ⟹ 2 r = 1 2 ⟹ r = 6