Tangents and Triangles
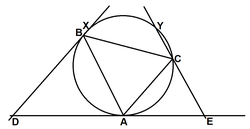 The tangent at
of the circumcircle of the triangle
is drawn. The points
and
are constructed on it such that
is parallel to
and that
is parallel to
. The lines
and
intersect the circle
again at
and
respectively.
The tangent at
of the circumcircle of the triangle
is drawn. The points
and
are constructed on it such that
is parallel to
and that
is parallel to
. The lines
and
intersect the circle
again at
and
respectively.
Given that , find .
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
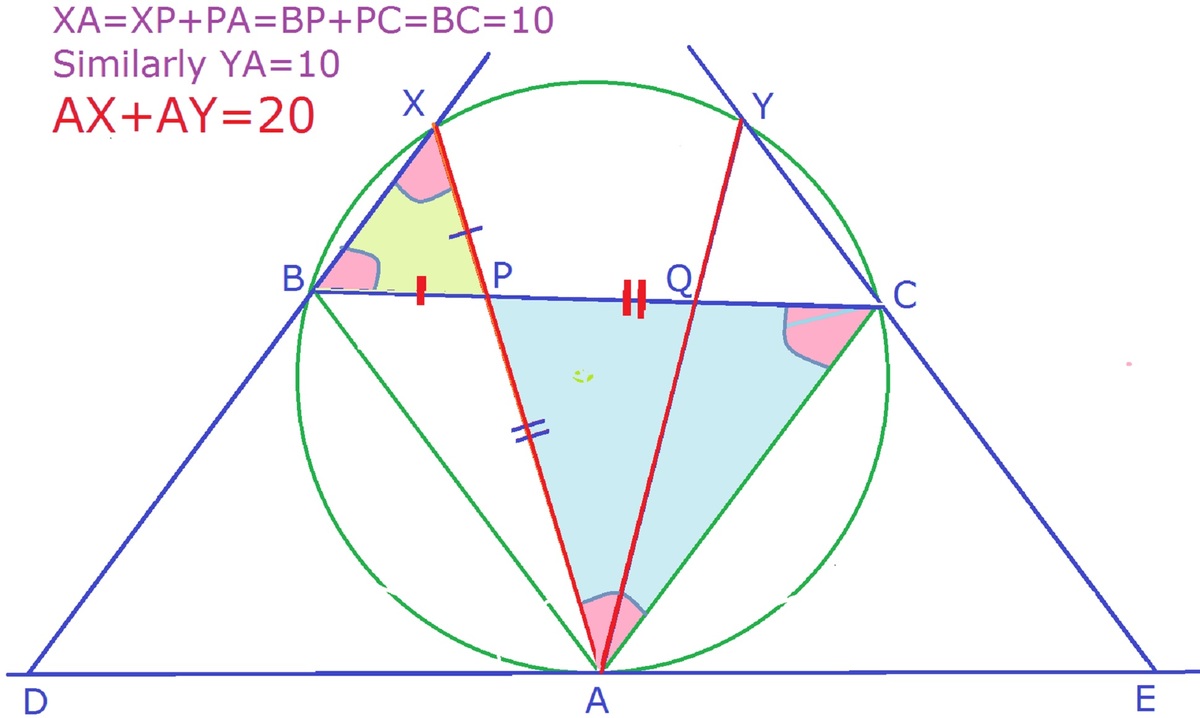
We consider A X first. ∠ A X C = ∠ A B C (angles in the same segment) and ∠ B X C = 1 8 0 ∘ − ∠ B A C (opposite angles in a cyclic quadrilateral), ∠ X B C = ∠ B C A (alternate angles).
Now, since ∠ A B X = ∠ B X C and B X is parallel to A C , we can conclude that A B X C is a isosceles trapezium (or trapezoid). Hence the diagonals are of the same length so A X = B C . Similar reasoning shows that A Y = B C .
Therefore A X + A Y = 2 B C = 2 0 , as required.