Tangling Circles

Geometry Level 5

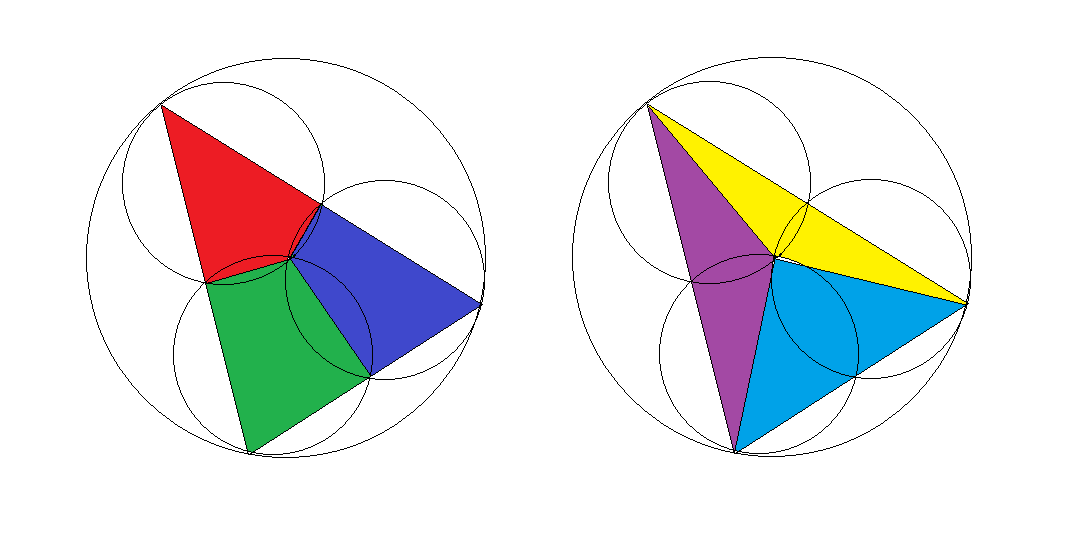
Three circles with the same radius intersect at the center of a bigger circle with twice the radius.

Lines are drawn from the intersection points where two small circles meet on the big circle such that they form a triangle, as shown above left. The triangle is then divided into 3 quadrilaterals by drawing the lines from the center of the big circle to the intersection points of the small circles: red, blue, and green regions.

Alternatively, the triangle can be divided into 3 smaller triangles by simply drawing the lines from the center to the vertices: yellow, purple, and cyan regions in the diagram on the right.

Suppose that the ratio of the area of the red region, the area of the dark blue region, and the area of the green region is $11:12:13$ .

Then, if the ratio of area of the yellow region, the area of the purple region, and the area of the light blue region is $a:b:c$ , where $\gcd(a,b,c) =1$ , compute $\frac{a+b+c}{3}$ .

The answer is 6.

2 solutions

Worranat Pakornrat
Jun 23, 2016

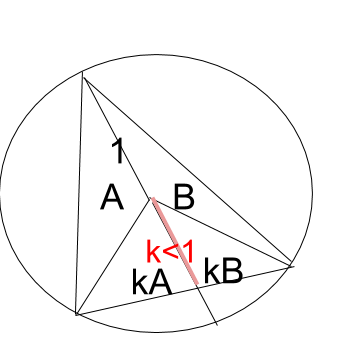
Since the distance from the big circle's center to each triangle's vertex is equal to the big radius, this is also the triangle's center.

Hence, the lines from this center to the bases of smaller triangles will act as their bisectors, halving the areas of the yellow, purple, and cyan isosceles triangles.

Furthermore, by comparing between the two diagrams, it is obvious that red area = half yellow + half purple; blue area = half yellow + half cyan; and green area = half cyan + half purple.

Let $x = yellow/2; y = purple/2; z = cyan/2$ . From the given ratio, we can formulate the equations for some constant $k$ :

$x + y = 11k$

$x + z = 12k$

$y + z = 13k$

Solving for the three variables, we will get $x = 5k; y = 6k; z = 7k$ .

As a result, the ratio of $Yellow : Purple: Cyan = 2x : 2y : 2z = 5 : 6 : 7$ .

The answer is, therefore, $\dfrac{5+6+7}{3} = \boxed{6}$ .

Moderator note:

Nice setup of the problem, with an easy area observation.

What are the necessary and sufficient conditions for such a triangle to exist? Note that the point of intersection (which is the circumcenter of the triangle) need not be within the triangle.

Thumbs up solved the same way

will jain - 4 years, 11 months ago

Hi, the problem does not have a solution. If it had one, it would be 1:2:3. However, this conflicts with the fact that the areas of small triangles have to satisfy triangle equality - any triangle has an area less than the sum of the other two triangles. This is even sufficient condition for the solvability, as we can take the limit case where circles are all at the same position and continously move them apart to acquire permissible values. The problem is nice; it would be worth to reformulate the ratios of quadrilaterals and post again.

Stanislava Sojáková - 4 years, 11 months ago

Thank you for your suggestion. Now I've adjusted the ratio such that the triangle exists without changing the answer. ;)

Worranat Pakornrat - 4 years, 11 months ago

Doesn't have the worth of geometry level 5

D K - 2 years, 10 months ago

Niranjan Khanderia
Jun 24, 2016

Each of the isosceles triangle is made up of two congruent right triangles.
Each of the quadrilateral is made by combining one of the right triangle from adjoining triangles.
Let the areas be represented by variables,.......2a=Yellow,........2b=Indigo,.........2c=Light Blue.
So areas Red=a+b=3k,.......Dark Blue=c+a=4k,.......Green=b+c=5k,..........k appropriate constant.
Adding and simplifying, a+b+c=k6, implies a=k,.......b=2k,.......c=3k.
So a : b : c :: 1 : 2 : 3 $\ \ \ \ \implies\ a * b * c = 1 * 2 * 3 = \Huge \ \ \ \color{#D61F06}{6}$

Tangling Circles

The answer is 6.

2 solutions

Moderator note:

0 pending reports