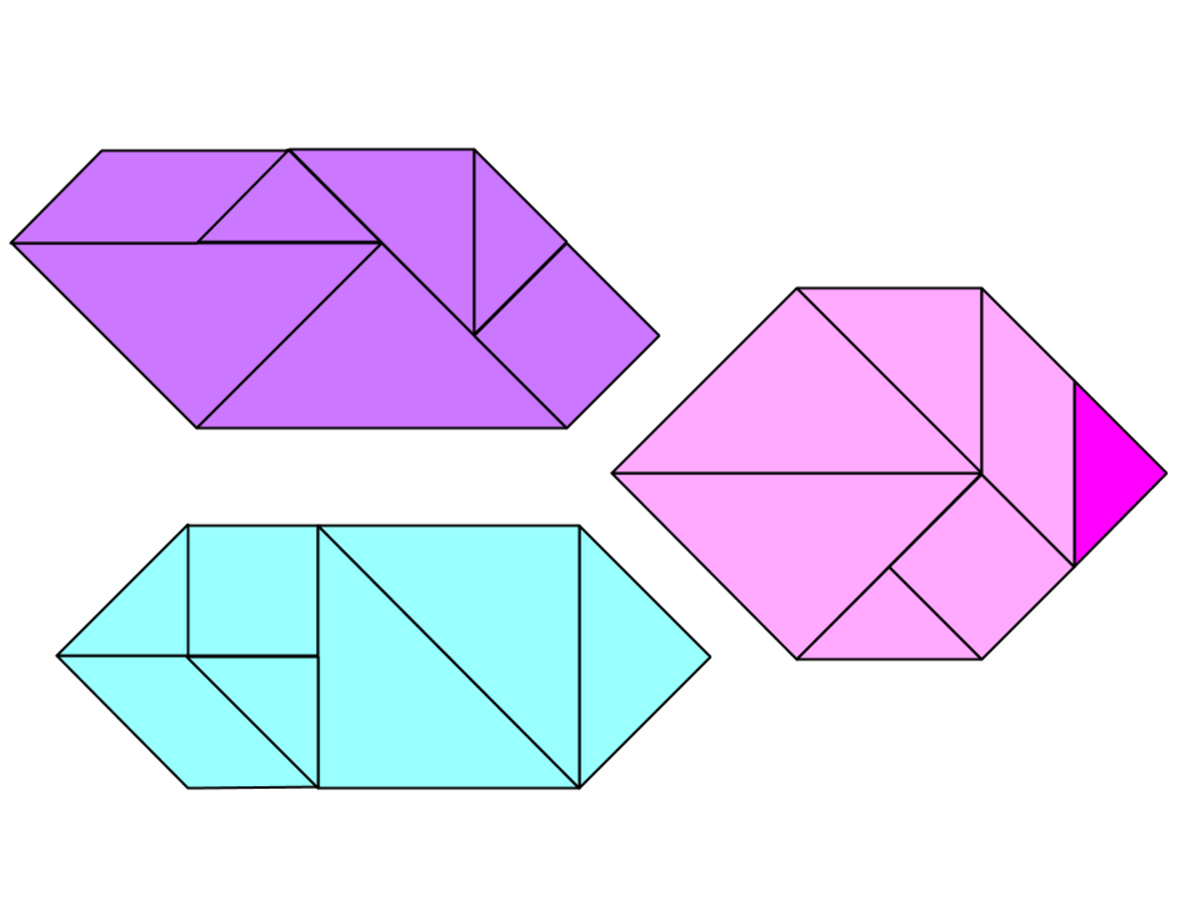
Tangram Geometry

Consider the tangram set, in which the large square can be split into 7 polygons - 5 triangles, 1 square, and 1 parallelogram.
If we use all 7 pieces to form a convex polygon, what is the greatest number of sides of this polygon?
7
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Tangrams have corners that are 45, 90 ,135 degrees. Any convex polygon of tangrams will have same corner angles of 45 ,90 ,135 because any larger combination at corners create a straight side 180 or a concave >180 angle that is not allowed by definition of convex. Since any polygon can be divided into triangles the sum of interior angles will given by 180*(n-2) so n=7 sides 900 degrees would require angles to include 6(135°)+1(90°) (like an equiangular octagon with 1 edge 2 corners erased and sides extended to point) and with the side lengths number of pieces is not possible to do without holes or leaving out a piece. However there are a few 6 sided solutions (one of which shows how a 7 sided figure could be made with 6 of 7 pieces (remove dark pink))