Tank Half Empty

$A_1$ : Cross-sectional area of the cylinder, $A_2$ : Cross-sectional area of the small hole at the bottom, $g$ : Acceleration due to gravity,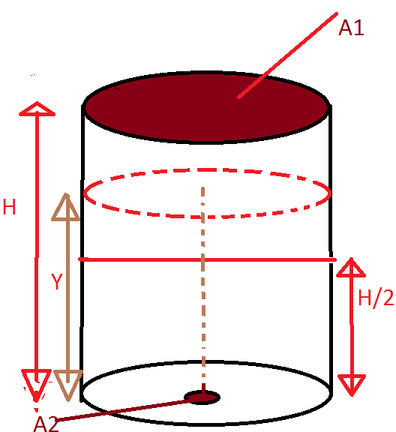 First of all, by applying the Continuity equation we can compute the value of $\frac { { A }_{ 2 } }{ { A }_{ 1} }$ i.e $\frac { { A }_{ 2 } }{ { A }_{ 1 } } =\frac { { V }_{ 1 } }{ { V }_{ 2 } }$ .Now from the figure we take a variable distance $y$ from the bottom of the cylinder given that the distance lies in between $\frac { H }{ 2 } <y<H$ . Since the water is flowing away from cylindrical container we make use of the negative sign in the continuity equation, it also denotes that water is decreasing from the container. With the aid of calculus we came to see that water is decreasing at a rate of $\frac { dy }{ dt }$ , from torricelli's theorem the velocity of water from the small orfice at the bottom is $\sqrt { 2gy }$ . Therefore the equation becomes $-{ A }_{ 1 }\frac { dy }{ dt } ={ A }_{ 2 }\sqrt { 2gy }$ , on rearranging we get $\frac { -dy }{ \sqrt { 2gy } } =\frac { { A }_{ 2 } }{ { A }_{ 1 } } dt$ by applying integrals on both sides with appropriate limits we get $\int _{ H }^{ \frac { H }{ 2 } }{ \frac { -dy }{ \sqrt { 2gy } } } =\frac { { A }_{ 2 } }{ { A }_{ 1 } } \int _{ 0 }^{ 5 }{ dt }$ for the time being let us take $\frac { { A }_{ 2 } }{ { A }_{ 1} }$ as a constant C i.e $\frac { { A }_{ 2 } }{ { A }_{ 1} }$ = $C$ on integrating we find the value of $C$ as $C =\quad \sqrt { \frac { H }{ g } } \quad \left[ \frac { \sqrt { 2 } -1 }{ 5 } \right]$ . Similarly we consider the other half of the cylinder, here also we take a variable distance $y$ but this time $y$ lies in between $0$ to $\frac { H }{ 2 }$ , and we make use of the continuity equation. By applying integrals on both sides, the equation becomes $\int _{ \frac { H }{ 2 } }^{ 0 }{ \frac { -dy }{ \sqrt { 2gy } } } =C\int _{ 0 }^{ T }{ dt }$ from this expression $T$ is the value which is to be determined and it is the remaining time taken to completely drain water from the half filled cylinder, On substituting the value of $C$ and integrating the equation( mentioned just above), we'll get the value of $T$ as $T=\frac { 5 }{ \sqrt { 2 } -1 } \quad \sim \quad 12 min$