Tanning around the earth
It's a lot easier to get a suntan in the summer than the winter. The suntanning issue (and the seasons) is due to the the tilt of the earth's axis with respect to the plane of the earth's orbit. The earth's axis is tilted 23 degrees with respect to the normal to the plane of its orbit. see here for a nice discussion and animation).
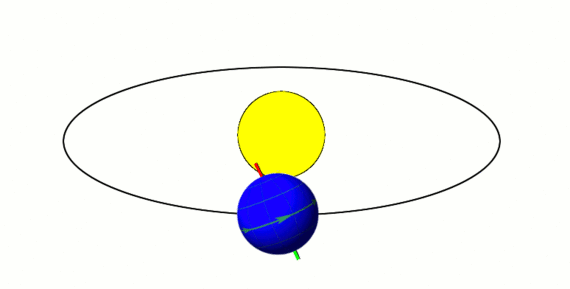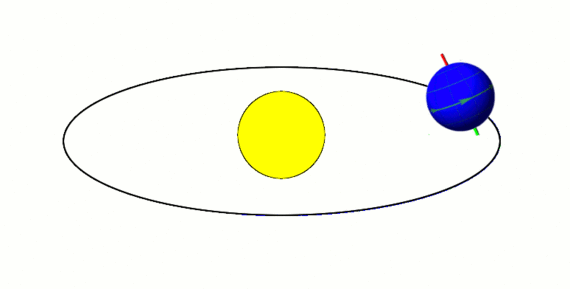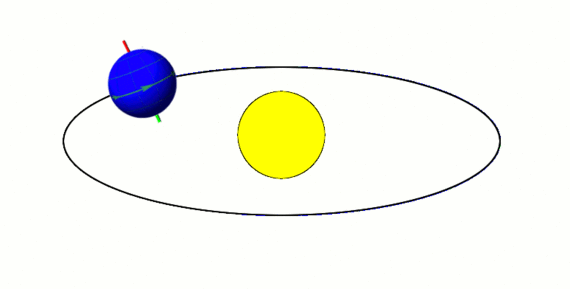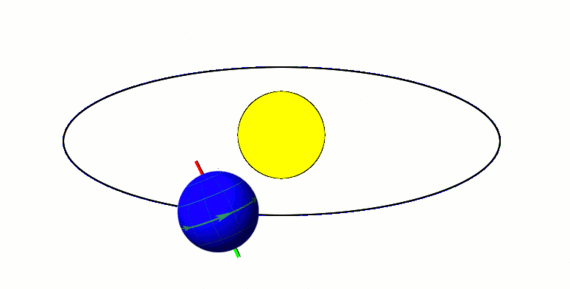
Consider someone who lives 23 degrees north of the equator. Let the maximum intensity of sunlight on the Earth's surface for this person during the summer day when the Earth's axis is tilted most towards the Sun be I s u m . Similarly I w i n will be the maximum intensity of sunlight during the winter day when the Earth's axis is tilted most away from the sun.
What is I w i n / I s u m ?
Details and assumptions
- You may consider the Earth as a perfect sphere and the orbit of the Earth as a perfect circle.
- Since the Sun is so far away, all the rays of sunlight may be considered to hit the Earth parallel to the orbital plane.
The answer is 0.695.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
In the summer, when the axis is tilted most towards the sun, the angle of the sun relative to the normal at 23 degrees north is 2 3 ∘ − 2 3 ∘ = 0 ∘ . Therefore, in the summer, the sun is shining directly above 23 degrees north, which is the maximum possible intensity. We will represent this with I s u m .
In the winter, when the axis is tilted most away the sun, the angle of the sun relative to the normal at 23 degrees north is 2 3 ∘ + 2 3 ∘ = 4 6 ∘ .
We wish to solve for the intensity of sunlight vertical to our location in winter. We split the rays of sunlight into horizontal and vertical components (relative to our location). Note that the sum of our components has intensity I s u m , since the sun's intensity directly shining at us is constant. Therefore our vertical component has intensity I s u m ⋅ cos 4 6 ∘ = I w i n .
Therefore I w i n / I s u m = I s u m ⋅ cos 4 6 ∘ / I s u m = cos 4 6 ∘ ≈ 0 . 6 9 5 .
In the summer,when the axis of the earth is tilted most towards the sun, the angle of the sun relative to the normal at the 2 3 ∘ mark is 2 3 ∘ − 2 3 ∘ = 0 ∘ Therefore,in the summer,the sun is shining directly over 2 3 ∘ N which is the maximum possible intensity.Let us represent this as I s u m . In the winter when the axis is tilted most away from the sun,the angle relative to the normal at 2 3 ∘ N is 2 3 ∘ + 2 3 ∘ = 4 6 ∘ . Let us denote the maximum possible intensity in winter as I w i n . We wish to solve for the intensity of sunlight vertical to our location in winter. We split the rays of sunlight into horizontal and vertical components (relative to our location). Note that the sum of our components has intensity I s u m , since the sun is shining directly on us at this instant and is constant. Therefore our vertical component has intensity I s u m × cos 4 6 ∘ = I w i n . Therefore I s u m I w i n = I s u m I s u m × cos 4 6 ∘ ⇒ I s u m I w i n = cos 4 6 ∘ ⇒ I s u m I w i n = 0 . 6 9 4 6 5 ⇒ I s u m I w i n ≈ 0 . 6 9 5
why will I_sum strike you directly? Does the earth tilt 23 degrees?
Well, Daniel, we know that the sun rays strike the tropics directly every year on two days i.e on the summer solstice on June 21 on the Tropic of Cancer and on the Winter Solstice on 22nd December on the Tropic of Capricorn. As we are dealing with the northern hemisphere, in the Summer the maximum intensity of the sun over Tropic of Cancer is on the Summer Solstice. Please answer me whether I am clear enough or not. I value your opinion.
The first thing to notice in this problem is the angle at which sun rays fall in each season. At tropics in summer the sun shines vertically overhead at 90 degrees. That is when the intensity is maximum and effective area minimum. At winter the sun rays fall at an angle in tropics. Remember as the earth rotates,the axis stays fixed. And sun rays travel in the plane of the orbit. Using these two hints and by simple geometry we see that at winter in tropics sun rays fall at 47 degrees to normal. Intensity when light shines at an angle theta is Imax*cos(theta). So Isum/Iwin=cos(47)=0.682
Lambert's law tells us that light intensity is proportional to cosine of angle between incidence and normal. In high summer, this angle of incidence is 0 (Earth is tilted towards sun so vertical rays hit the tropic line). Cos(0)=1. In peak of winter, angle of incidence is 2*23=46 degrees. Cos(46)=0.695. Hence ratio is 0.695.
In summer the intensity is Isum so for winter Iwin=Isum cosx Iwin/Isum=cos46=0.69
During the summer, the ray of the sun will strike perfectly normal to said person, because he resides 2 3 degrees above the equator, which is in turn 2 3 degrees below the line of direct sunlight.
In the winter, the sunlight strikes at an angle 2 3 + 2 3 = 4 6 to the normal, because the person is 2 3 degrees above the equator, which is in turn 2 3 degrees above the line of direct sunlight.
Thus, the ratio I w i n / I s u m = cos 4 6 = 0 . 6 9 5
P ⋅ A = I P , A , and I stand for power and area vector, and intensity respectively. In summer, the earth is tilted towards the sun, and thus the person lies on the horizontal line connecting the centers of the earth and the sun. In winter, the earth is tilted away from the sun, and thus the person lies 4 6 ∘ above the horizontal line connecting the centers of the earth and the sun. Thus, I s u m = P ⋅ A = P A c o s ( 0 ∘ ) and I w i n = P ⋅ A = P A c o s ( 4 6 ∘ ) . I w i n / I s u m = P A c o s ( 4 6 ∘ ) / P A c o s ( 0 ∘ ) = 0 . 6 9 5