Tato Red Envelope for Chinese New Year
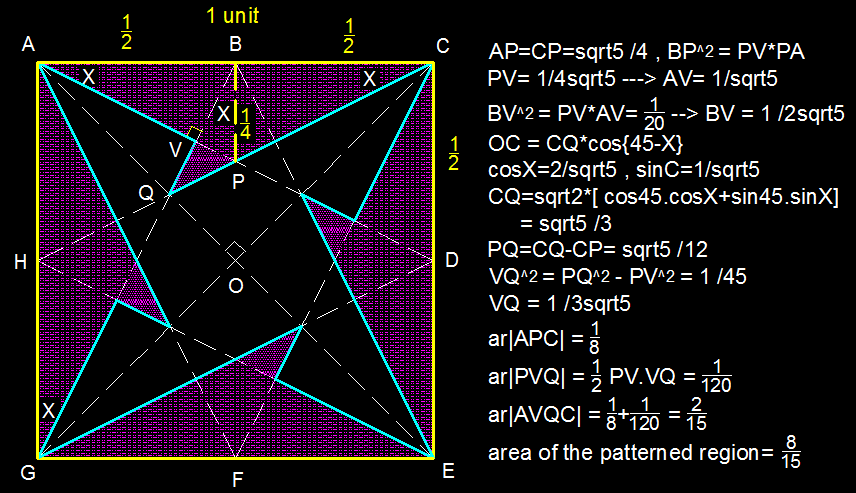
Chinese New Year is about to come soon. Michael did not have any red envelope in his house, so he started with a smooth origami paper. He created the Tato envelope, which resembles a unit square as shown above, where and are the midpoints of , , and , respectively. Each of the lines within the square is projected from the given points.
What is the area of the patterned region in the diagram? If your answer can be expressed as , where and are coprime positive integers, evaluate .
Fun Hint: Figure out how to create the Tato envelope as shown above. Before reaching the final steps to do some computation, carefully observe the angles of the polygons. This should help you answer the problem.
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

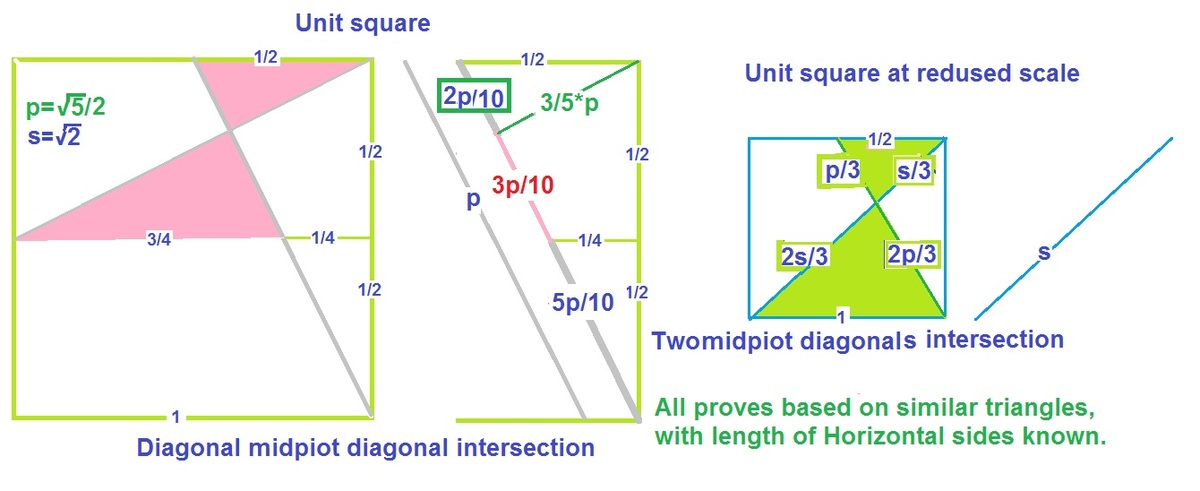
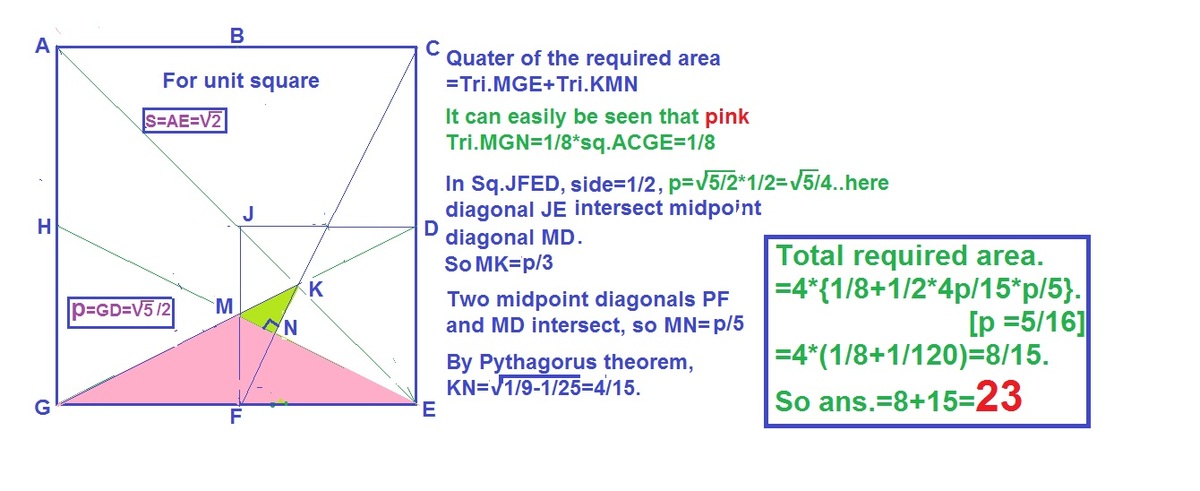
By symmetry, the areas of △ X H G and △ G Z F are each repeated 4 times in the diagram below. So the basic idea will be to find the area of each triangle, add them, and multiply the result by 4.
Suppose the unit square is oriented on the coordinate plane so G is at (0,0) and C is at (1,1). Given this setup, we first want the coordinates of points X , Y , and Z .
The location of X occurs at the intersection of lines y = 2 x and y = − 2 1 x + 2 1 . Substituting, 2 x = − 2 1 x + 2 1 so 2 5 x = 2 1 and therefore x = 5 1 . This also implies y = 2 x = 2 ⋅ 5 1 = 5 2 . Therefore X is at ( 5 1 , 5 2 ) .
Y is symmetrical to X across the line y = x , so the point is simply the reflection such that the x and y coordinates swap: ( 5 2 , 5 1 ) .
The location of Z occurs at the intersection of lines y = − x + 1 and y = 2 1 x . Substituting, − x + 1 = 2 1 x and so 2 3 x = 1 implying x = 3 2 . Since y = − x + 1 this means y = 3 1 . Therefore Z is at ( 3 2 , 3 1 ) .
Now we can find the areas using the triangle formula 2 1 ⋅ base ⋅ height :
For the area of △ X H G , using the base at G H (which has a length of 2 1 ) and height dropping a perpendicular from X to G H (which by the coordinate X has a length of 5 1 ) , the area is 2 1 ⋅ 2 1 ⋅ 5 1 = 2 0 1 .
For the area of △ G Z F we can use the base at G Z and height at Y F . The length of each can be found with the distance formula and the coordinates calculated above. The length of G Z between (0,0) and ( 3 2 , 3 1 ) is 3 5 . The length of Y F between ( 5 2 , 5 1 ) and ( 2 1 , 0 ) is 2 5 1 . Using these to find the area results in 2 1 ⋅ 3 5 ⋅ 2 5 1 = 1 2 1 .
Adding these areas gets 2 0 1 + 2 0 1 = 1 5 2 ; multiplying by 4 (since each triangle occurs 4 times in the patterned area) gets a final result of 1 5 2 ⋅ 4 = 1 5 8 . Therefore the answer desired is 8 + 1 5 = 2 3 .