The Teardrop
Let c be a negative constant. When the two parabolas y = x 2 + c and x = y 2 + c are tangent, the area of the region of overlap can be expressed as B A , where A and B are coprime positive integers. Find A + B .
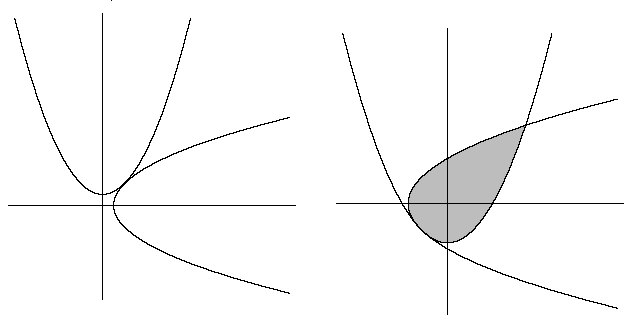
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Looks like all that remains is:
Area = 2 ∫ − 0 . 5 1 . 5 ( x − x 2 + 4 3 ) d x
Log in to reply
It was getting late here. Thanks, I thought this wouldn't work.
- I think we should add in c < 0 to ensure we are in the image on the right.
- I simplified the expression into just B A . We typically find that it is best to leave the expression simple.
I was on the right track with f(a)=g(a) and f'(a)=g'(a) where g is the inverse and how C is a certain value I have to find, but I didn't know where to go from there.
Let the two parabolas be y 1 = x 2 + c and y 2 2 = x + c and the point their tangents touch be P ( a , b ) . Then, y 1 ( a ) = y 2 ( a ) and d x d y 1 ∣ ∣ ∣ ∣ x = a = d x d y 2 ∣ ∣ ∣ ∣ x = a .
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ d x d y 1 = 2 x 2 y 2 d x d y 2 = 1 ⟹ d x d y 2 = 2 y 2 1 ⟹ d x d y 1 ∣ ∣ ∣ ∣ x = a = 2 a ⟹ d x d y 2 ∣ ∣ ∣ ∣ x = a = 2 b 1 ⟹ 2 a = 2 b 1 ⟹ a b = 4 1
From symmetry, we can assume that a = b , ⟹ a = b = − 2 1 as P is in the third quadrant. From y 1 ( a ) = b = a 2 + c ⟹ c = − 4 3 .
We note that the area required is twice that bounded by either parabola and the orange straight line y = x . Since it is easier to work with purple parabola y = x 2 − 4 3 , we have the area:
A = 2 ∫ − 2 1 2 3 ( x − x 2 + 4 3 ) d x = 2 [ 2 x 2 − 3 x 3 + 4 3 x ] − 2 1 2 3 = 3 8
⟹ A + B = 8 + 3 = 1 1