Teetering Triangle

Geometry Level pending

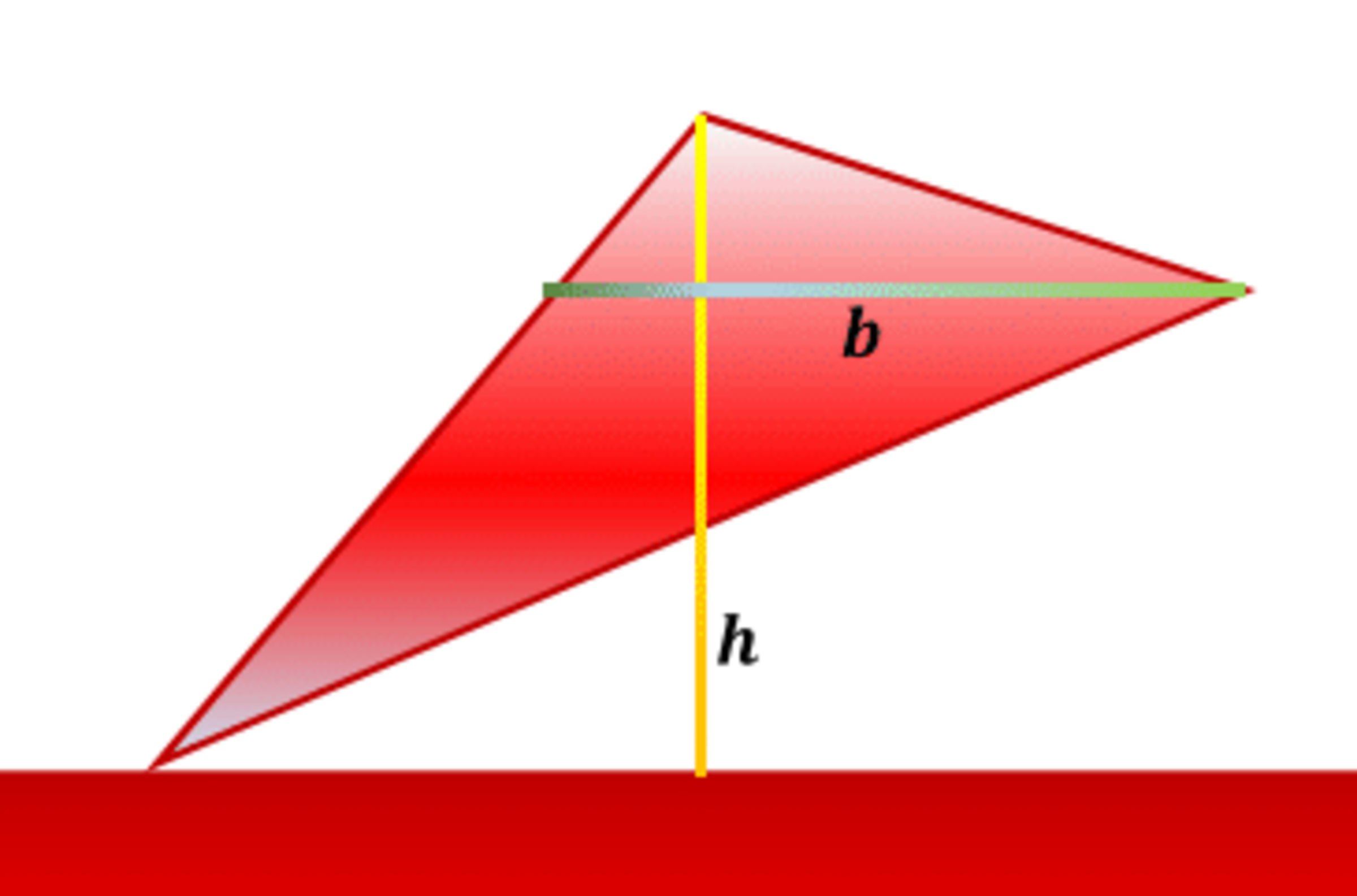
"Area of a triangle is $\dfrac 12 bh$ . In this $h$ is the height. It's what you get when you go from the top point of the triangle all the way to the ground going straight down. $b$ is what they call the base. It is always horizontal and goes from the point of the triangle which you can go into the triangle from. It goes all the way to the other side of the triangle."

Does the above description give the correct value for the area of the triangle?

Sometime, but it's a lucky chance Yes Most of the time, but there are exceptions No

1 solution

Marta Reece
May 15, 2017

To see that it's true, divide the triangle into two triangles along its "base" and you can see that total area is the sum of areas the triangles and is equal to:

$A=\dfrac12 bh_1+\dfrac 12 bh_2=\dfrac12 b(h_1+h_2)=\dfrac12 bh$

Teetering Triangle

1 solution

0 pending reports