Telescoping Series 2 – Future Terms
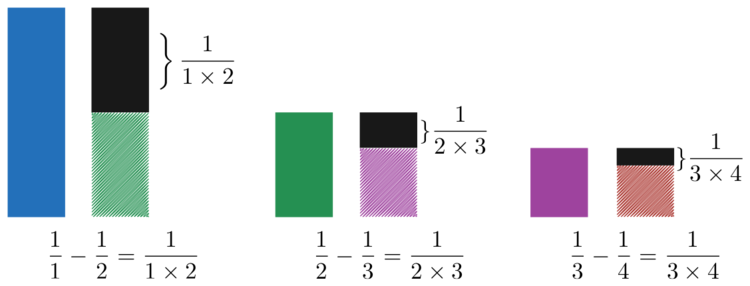 Consider the following pattern:
Consider the following pattern:
1 × 2 1 2 × 3 1 3 × 4 1 ⋮ = 1 1 − 2 1 = 2 1 − 3 1 = 3 1 − 4 1
Following the pattern above, if 1 1 × 1 2 1 = a 1 − b 1 , what are the values of a and b ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
a=11& b=12
a=11 and b=12
a=11 and b=12
The problem can be solved by this equation. {1/(n*(n+1))=(1/n)-(1/n+1)}. Though this is not required because the theory and examples are given. But if they were not there then this equation is the best method.
a=11 and b=12
a=11 n b=12
a = 11 , b=12
a=11,b=12
a=11 & b=12
a=11& b=12
a=11 and b=12
a=11 b=12
a=11& b=12
i solved it again
see tipe
So easy??????!!!!
a=11& b=12
a=11 and b=12
a = 11 and b = 12
it follows a logic so a=11 and b=12
a=11 and b=12
a=11, b=12
I think that 's right!
a=11, b=12
Actually the series is a telescoping series which is a series where each term can be represented in the following way , u k = t k − t k + 1 . . . . . . . . ( 1 ) Where t k is some series.
For this series we can see that t k = n 1 so u k = n × ( n + 1 ) 1
so from (1) it can be seen that n × ( n + 1 ) 1 = n 1 − n + 1 1
The theory is 1/n(n+1))=(1/n)-(1/n+1) and the the answer will be a = 11 and b = 12
when 1/2-1/3 then a=2, b=3 this way 1/11-1/12 gets a=11 b=12
By observing the patter it is like a series with nth term 1/n-1/n+1
its very easy.......i simply looked at the denominator's pattern
I actually just followed the patterns on the denominators.
by solving 1/11-1/12 we get result as 1/(11*12) so a=11& b=12
we know (1/n)-(1/(n+1)) = 1/(n*(n+1)) so in this case n = 11. so a=11 and b=12
same solution because the result has to be positive so the bigger fraction first
Follow the pattern. 1/n - 1/(n+1) = 1/n*(n+1)
The problem can be solved by this equation. {1/(n*(n+1))=(1/n)-(1/n+1)}. Though this is not required because the theory and examples are given. But if they were not there then this equation is the best method.
this problem should have been there without all that theory and examples thers nothing to do just write 1 as 12-11 and cancel
1/11- 1/12 ,shows a=11 and b=12 Ans
easy to solve. good
similar to given details, 1/11- 1/12 ,shows a=11 and b=12 Ans
K.K.GARG,India
a=11 and b=12
The problem solve by this equation. {1/(n*(n+1))=(1/n)-(1/n+1)}