Ten circles
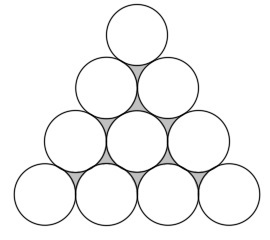 Ten circles of equal radii are arranged as shown. If the area of the shaded region is
9
3
−
2
9
π
, what is the area of the ten circles?
Ten circles of equal radii are arranged as shown. If the area of the shaded region is
9
3
−
2
9
π
, what is the area of the ten circles?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Solve this @Krishna Karthik
Log in to reply
@Percy Jackson Done bro. :)
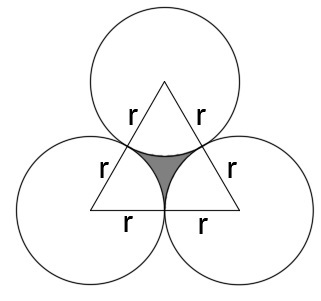 Consider my diagram. The area of one shaded part is
9
9
3
−
2
9
π
=
3
−
2
π
. The area of one shaded part is equal to the area of the equilateral triangle minus the area of the three circular sectors. We have
Consider my diagram. The area of one shaded part is
9
9
3
−
2
9
π
=
3
−
2
π
. The area of one shaded part is equal to the area of the equilateral triangle minus the area of the three circular sectors. We have
3 − 2 π = 4 3 ( 2 r ) 2 − 3 ( 3 6 0 6 0 ) ( π ) ( r 2 )
3 − 2 π = 3 r 2 − 2 π r 2
3 − 2 π = r 2 ( 3 − 2 π )
r 2 = 3 − 2 π 3 − 2 π = 1
r = 1
So the area of the ten circles is 1 0 ( π ) ( 1 2 ) = 1 0 π
Here's my two cents.
So, consider the triangle drawn in the diagram below:
Such a triangle partitions the circles so easily; the area of the triangle above basically constitutes of the shaded area, and the area of the circles within the triangle.
The triangle's vertices are placed at the centres of each end-circle. Each segment therefore goes through the centres of each circle, and just partitions them into halves, with the centre circle untouched.
The area of the equilateral triangle above can be found by:
A t = 4 3 ( 6 π 2 )
To equate the area of the equilateral triangle to the areas of the half circles inside and the shaded area:
A t = A s + A c
Counting the half-circles in the equilateral triangle:
4 3 ( 6 π 2 ) = 9 3 − 2 9 π + 6 2 1 π r 2 + 3 6 1 π r 2 + π r 2
Simplifying and solving yields r = 1
So the area is 1 0 π