Tension and acceleration on inclined plane
Consider a set-up as shown in the figure below.
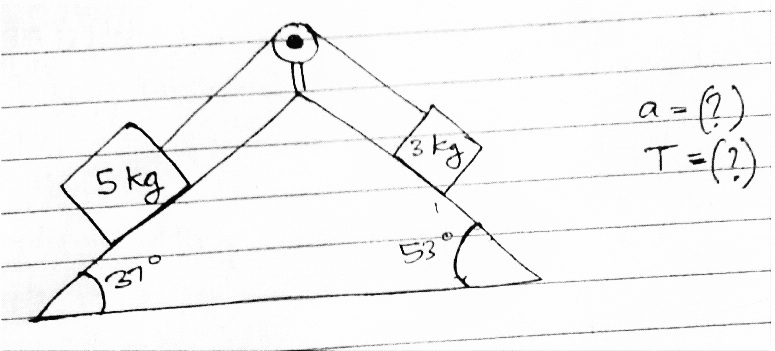
If the tension in the string is T N and the acceleration of the whole system is a m/sec 2 , the submit the value of T + a .
Details and assumptions :-
- Assume that the pulley and strings shown in the figure are massless.
- Assume that the surface of the inclined plane is frictionless.
- Take g (acceleration due to gravity) as 1 0 m/sec 2 .
- Round your answer off to the nearest integer.
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The vertical component of the force exerted by
5
kg
block =
mg
sin
θ
=
5
×
1
0
×
sin
(
3
7
)
°
=
3
0
N
.
The vertical component of the force exerted by
3
kg
block =
mg
sin
θ
=
3
×
1
0
×
sin
(
5
3
)
°
=
2
4
N
.
So, the net force is
3
0
−
2
4
=
6
N
.
Now,
F
a
a
=
ma
=
5
+
3
6
=
0
.
7
5
m/sec
2
Now, since the vertical component of the force exerted by the
5
g
block is more,
mg
sin
θ
−
T
3
0
−
T
T
T
=
ma
=
5
×
0
.
7
5
=
3
0
−
3
.
7
5
=
2
6
.
2
5
N
So, T + a = 2 6 . 2 5 + 0 . 7 5 = 2 7
For 5kg box, we will get:
5 × 1 0 sin 3 7 ° − T = 5 a . . . ( 1 )
For 3kg box, we will get:
T − 3 × 1 0 sin 5 3 ° = 3 a . . . ( 2 )
Solving ( 1 ) and ( 2 ) , we get:
a = 4 3
T = 4 1 0 5
∴ a + T = 4 1 0 8 = 2 7
Note: a = acceleration of box and T = Tension
sin 3 7 ° = 5 3 and sin 5 3 ° = 5 4 .