Tension? Brilliant
A 3D model of brilliant.org's logo of mass 3 kg has been hung onto a flat surface using two ropes of negligible mass. Assuming the force of gravity = , what is the sum of the tensions of the rope (in )?
Round to 2 significant digits
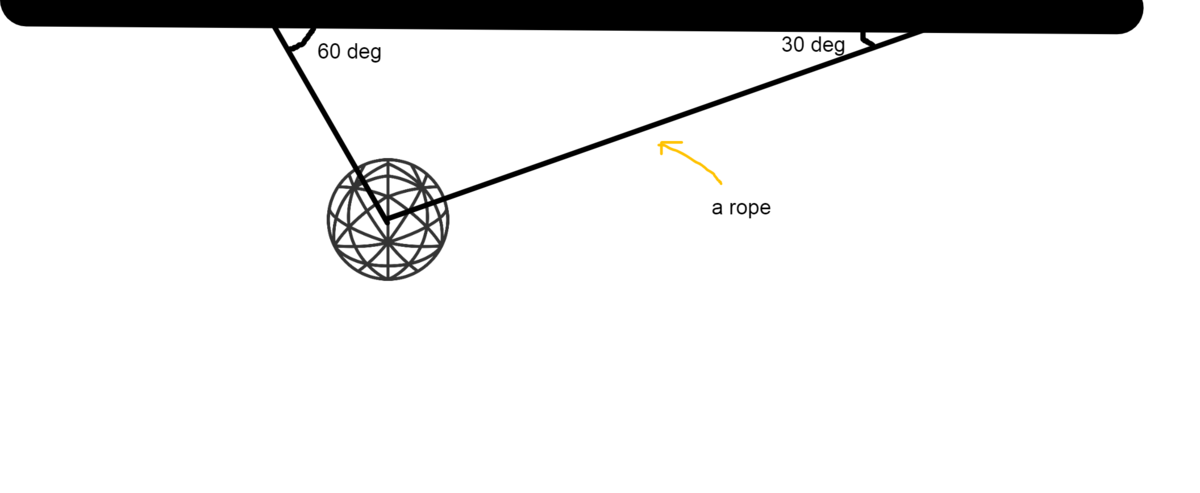
The answer is 41.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the left-side string tension be T 1 and the right-side string be T 2 . The Brilliant sphere will remain in static equilibrium according to Σ F x = 0 , Σ F y = 0 , or :
Σ F x ⇒ T 1 cos ( π / 3 ) − T 2 cos ( π / 6 ) = 0 ; (i)
Σ F y ⇒ T 1 sin ( π / 3 ) + T 2 sin ( π / 6 ) − m g = 0 (ii)
We first find that T 1 = 3 T 2 from (i). If we substitute this expression into (ii), then we obtain:
3 T 2 ( 3 / 2 ) + ( 1 / 2 ) T 2 = ( 3 ) ( 1 0 ) ⇒ 2 T 2 = 3 0 ⇒ T 2 = 1 5 , T 1 = 1 5 3 newtons.
Hence, T 1 + T 2 = 1 5 ( 3 + 1 ) = 4 0 . 9 8 newtons.