Tension in A Rotating Loop?
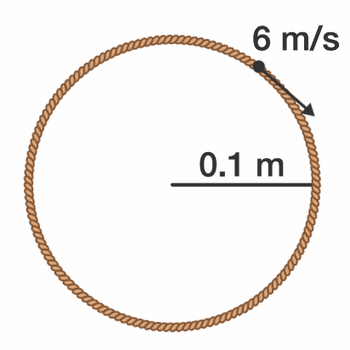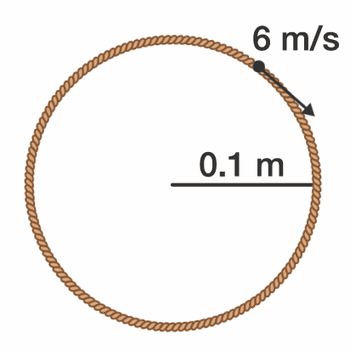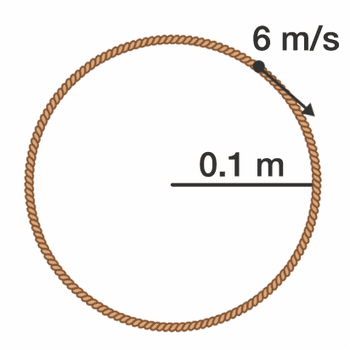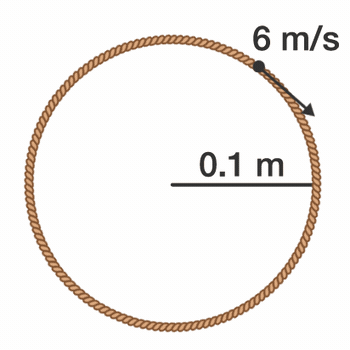
A rope loop of radius r = 0 . 1 m and mass m = 5 0 π g rotates on a frictionless table such that the tangential velocity of any point on the loop is v tangential = 6 m / s .
Find the tension in the loop (in Newtons).
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
You have a misprint: answer is 9N, not 900N.
Log in to reply
Yes. Sorry Sir
Log in to reply
Also, why do you use points (.) instead of multiplication × in the fractions ?
Otherwise, it is ok toh?
The code for ≈ is \approx .
Can I have an easier explanation. Please?
Log in to reply
Yes, we can solve this problem very easily by drawing the free body diagram of half rope and writing Newton's laws equation for it.
Either I missed a decimal, but I got 90 N? 50 g is 0.05 kg perhaps this is the mistake?
Log in to reply
No, the solution is correct, I just doublechecked it.
@Md Zuhair - hi, I see the prove. It is delicate besides one point. How can we get two Tention at A and B but have different directions
Log in to reply
Thanks.Yes. Tension is an internal force and think about the portion AB. First of all ,tension at A pulls the part AB in anti clockwise direction where as B pulls the part AB in clockwise direction. so it cancels out to zero.
If i answered your question correct then it is ok, or else please explain your question sir.
m = 50 pi/1000 kg = 25/1000 * 2pi kg dm = 25/1000 dt, with t being "theta" T sin(dt/2) 2 = dm v²/r = 25/1000 dt v²/r, with sin(dt) = dt T dt/2 2 = 25/1000 dt v²/r T = 25/1000 36/0.1 T = 25 36/100 = 9N
Thank you for a great explanation
Shouldnt be 18 N? The centrepetal force is acting on two ends of the string, so 2Tsin(theta)=2F.
Log in to reply
Centripetal force is acting along the radius and away from the centre. It is balanced by components of tension,
As I remember from high school F=ma; a=V/r so F=m V/r. Do not forget to put m in kilogram instead of gram m=50π/1000=0.05π. F= 0.05п 6/0.1=3π=3*3.14=9 The answer is 9H. Regards, Serhiy
Here in the figure, we have a loop and we took an elemental part magnified its view as the above picture.
You can see that Tension T is acting on the arc, and it is making an angle θ with the center.
So breaking up the rectangular components of the tension, we have
T cos θ = T cos θ which cancel out each other.
We are left with
2 T sin θ which will balance the centrepetal force r m v 2 .
⟹ 2 T sin θ = r m v 2 . . . ( i )
where m is the mass of that small portion of the loop.
So, m = 2 π r M × d l ⟹ 2 π r M . d l
Here d l is the arc length of the small portion.
We know d l = R 2 θ
Putting d l , We get
m = 2 π r M . r . 2 θ ⟹ π M θ
Putting values of m in (i)
We get
2 T sin θ = r m v 2 ⟹ 2 T sin θ = r . π M . θ . v 2
As θ is small, Using small angle approximation we have
sin θ ≈ θ [Actually not exactly equal]
We have
⟹ 2 T . θ = r . π M . θ . v 2
⟹ 2 T = r . π M v 2
⟹ T = 2 r . π M v 2
So we have our Tension as T = 2 r . π M v 2
Putting the values of the question, we get 9 N