Tension in a Uniform Thread!
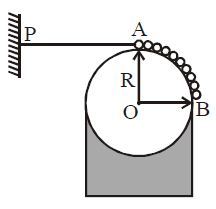 A uniform flexible chain of mass
m
and length
L
(
≤
2
π
R
)
rests on a fixed smooth cylindrical surface of radius
R
such that one end
A
of the chain is at the top of the cylinder while the other end
B
is free. The chain is held stationary by a horizontal thread
P
A
as shown in the figure. Calculate the Tension
(
T
)
in the thread.
A uniform flexible chain of mass
m
and length
L
(
≤
2
π
R
)
rests on a fixed smooth cylindrical surface of radius
R
such that one end
A
of the chain is at the top of the cylinder while the other end
B
is free. The chain is held stationary by a horizontal thread
P
A
as shown in the figure. Calculate the Tension
(
T
)
in the thread.
Assume α = R L .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Consider a tiny part of the chain, from stationary condition we have
T ( θ + δ θ ) + λ R g s i n ( θ ) δ θ = T ( θ )
d θ d T = − λ R g s i n ( θ )
T = λ R g c o s ( θ ) + C
we know that T=0 when θ = R L so C = − λ R g c o s ( θ )
and, finally, tension in the thread is equal to that in the chain at the highest point
F = T ( θ = 0 ) = λ R g ( 1 − c o s ( α ) ) = m g 2 α s i n 2 ( 2 α )
θ is measured from the top of the cylinder.
Next time use \sin for sin θ and \mathrm{d} for d θ . Cheers!
Oh I assumed the chain didn’t have tension 😂
L must be equal to 2 π ⋅ R and not ⩽ 2 π ⋅ R as, if L ⩽ 2 π ⋅ R , then we won't be able to make a perfect substitution sin ( 2 π ) = R L .
The solution is very simple. If you follow the Golden Rule,then the virtual work done by this force T - (dA=Tds) will be equal to the change in the potential energy dU of the small piece of the rope with the mass m ds/L. transfered from the point B to the point A . Hence dA = Tds= dU=mgds R/L (1 - cos L/R). And T= mgR/L (1- cos L/R).
Can you please specify what is d A and T d s ?
Log in to reply
dA is an elementary work done by the force T on the infinite small (virtual) displacement ds. That is why we use the evident equation dA= Tds.
Log in to reply
OK.... Thanks. You used Work Energy Theorem right(that Golden Rule)?
So, how can T − d A be a force?
