Terminal velocity
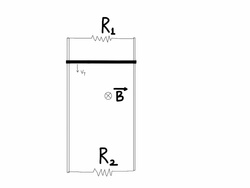 A system of long, parallel conducting rails is set up in the vertical plane and joined at both the ends by resistors as shown in the figure. A uniform magnetic field exists perpendicular to the plane of the rails denoted by
. A rod whose length is equal to the separation between the rails is allowed to fall freely and attain a terminal velocity. If the powers dissipated by the resistors
and
at steady state are
and
respectively, then what is the terminal velocity of the rod?
A system of long, parallel conducting rails is set up in the vertical plane and joined at both the ends by resistors as shown in the figure. A uniform magnetic field exists perpendicular to the plane of the rails denoted by
. A rod whose length is equal to the separation between the rails is allowed to fall freely and attain a terminal velocity. If the powers dissipated by the resistors
and
at steady state are
and
respectively, then what is the terminal velocity of the rod?
Details and Assumptions
- The length and mass of the rod are 1 m and 0.2 kg.
- The acceleration due to gravity is .
- The magnitude of the magnetic field is 0.6 T.
- The rails are long enough so that the steady state conditions can be easily analysed.
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
At steady state, by conservation of energy the rate of work done by the falling rod d t d W = m g v t e r m i n a l is equal the power dissipated by the two resistors R 1 and R 2 , P = 0 . 7 6 + 1 . 2 = 1 . 9 6 W . Therefore:
d t d W = P m g v t e r m i n a l = P ⇒ v t e r m i n a l = m g P = 0 . 2 × 9 . 8 1 . 9 6 = 1 m / s