Terminal velocity of an object on an inclined plane?
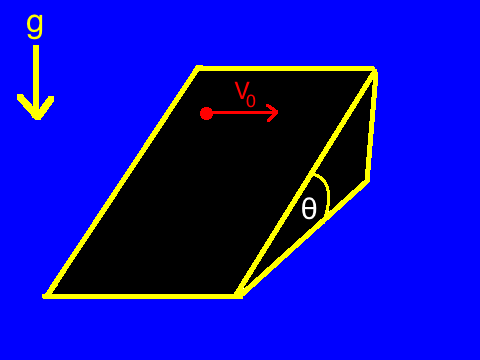 An object is on an inclined plane of angle
θ
with the horizontal. It is given an initial velocity of
V
0
in the sideways direction (i.e. perpendicular to the down-hill direction). If the coefficient of friction is
μ
=
tan
θ
, then find the terminal velocity of the object. (Neglect air resistance.)
An object is on an inclined plane of angle
θ
with the horizontal. It is given an initial velocity of
V
0
in the sideways direction (i.e. perpendicular to the down-hill direction). If the coefficient of friction is
μ
=
tan
θ
, then find the terminal velocity of the object. (Neglect air resistance.)
If the terminal velocity can be expressed as V terminal = k V 0 and k ⩾ 0 , then find k .
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is long. You have easier methods....
Let x be the direction down the plane. At any moment, the acceleration in x direction is the same as the retardation in tangential direction. So the magnitude of change in velocity in x direction is the same as magnitude of change in velocity in tangential direction(which is simply the change in net velocity). Since the terminal velocity will be in x direction, v x − 0 = v 0 − v x ⟹ v x = v terminal = 2 v 0
can you explain why?
Let x be the sideways direction, and let y be the down-hill direction. ( V x and V y are the components of velocity in those directions.)
The frictional force will be F f = m g μ cos θ = m g sin θ ... Since friction points in the direction opposite to the motion, we have F f F f . x = V x 2 + V y 2 V x and F f F f . y = V x 2 + V y 2 V y
Therefore the equations which describe the motion are:
d t d V x = − g sin θ V x 2 + V y 2 V x
d t d V y = g sin θ ( 1 − V x 2 + V y 2 V y )
We can eliminate the time dependence to get a differential equation for only V x and V y like this:
d V x / d t d V y / d t = d V x d V y = V x 1 ( V y − V x 2 + V y 2 )
A little thought will show this is a homogenous differential equation, and so it can be separated if we make the substitution u = V x V y and d V y = u d V x + V x d u
When you separate the equation you will get V x d V x + 1 + u 2 d u = 0
Integrating this gives ln ∣ V x ∣ + ln ∣ u + u 2 + 1 ∣ = C 0 = ln ∣ V y + V x 2 + V y 2 ∣
Which means that V y + V x 2 + V y 2 = C
We use the initial condition V y ( V x = V 0 ) = 0 to find the constant is C = V 0
Now we use the condition that the terminal velocity will be when V x = 0 to find V t e r m i n a l = V y ( V x = 0 ) = 0 . 5 V 0