Terrible Twins
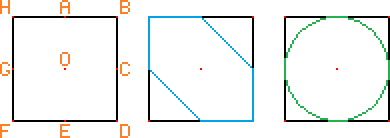
Two twins, Tom and Tyler are going to the park to play. Being competitive siblings, they devise a race around the square park which is labelled in the diagram below from A to H around the perimeter and has centre O.
Tom will run in a straight line from A to C to D to E to G to H to A, as shown in the blue diagram. Tyler will run in a perfect circle from A with centre O, passing the points C,E & G before returning to A, as shown in the green diagram.
Being twins, they run at the same constant speed. However, Tom must complete 9 laps whilst Tyler completes 10 . Who will win the race?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Given that they run at the same constant speed - we have to compare the distances they run.
Whoever has less to cover will win the race.
Tyler has to run 10 laps * 2*PI * R (radius of the green circle) ≈ 62.8 x R
Tom has to run 9 laps * (4 R + 2 2 2 ) ≈ (36 + 9 * 2 ) x R
Comparing the two (and getting rid of R), we see that the distance covered by Tyler ≈ 62.8 while Tom has ≈ 48,72
Therefore Tom has less to run and wins !