Tessellate S.T.E.M.S. (2019) - Computer Science - School - Set 4 - Objective Problem 2
You are given the following undirected unweighted graph.
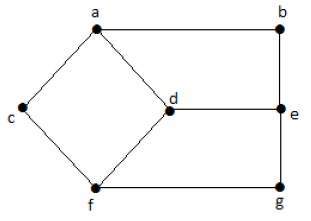
You have to write a number on each vertex of the graph. Each number should be 1 , 2 , or 3 . The graph becomes beautiful if for each edge the sum of numbers on vertices connected by this edge is odd. What is the number of possible ways to write numbers 1 , 2 , or 3 on vertices so the graph becomes beautiful.
This problem is a part of Tessellate S.T.E.M.S (2019)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Brute force (there are only 3 7 = 2 1 8 7 cases):
Length ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ Table ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ If ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ And @@ Table ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ OddQ [ t [ [ e [ [ 1 ] ] ] ] + t [ [ e [ [ 2 ] ] ] ] ] , ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ e , ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 1 1 2 3 4 4 5 6 2 3 4 5 6 5 6 7 7 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ , t , Nothing ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ , { t , Tuples [ { 1 , 2 , 3 } , 7 ] } ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⟹ 2 4
First, we partition the graph into even vertices (which will be numbered 2 ) and odd vertices (which will be numbered 1 or 3 ). We must do this in such a way that no two even vertices are adjacent and no two odd vertices are adjacent.
- If d is odd then a , e , f , have to be even and b , c , g have to be odd.
- If d is even then a , e , f have to be odd and b , c , g have to be even.
Thus, in one case there are three odd vertices and in the other case there are four. Since it doesn't manage whether odd vertices are numbered 1 or 3 , this leaves 2 3 + 2 4 = 8 + 1 6 = 2 4 possible graphs.
A second solution: We wish to find a two-coloring of this graph (with one color representing even numbers and the other representing odd numbers). This ensures that no two odd vertices are adjacent and no two even vertices are adjacent. But we are give a bipartite graph with the parts { a , e , f } and { b , c , d , g } . Since it is connected graph, this is the only bipartition. Therefore the only way to two-color this graph is to assign one color to a , e , f and another to b , c , d , g . Reason as before with respect to the odd vertices to arrive at 2 3 + 2 4 = 2 4 .
The only possible ways to make an odd sum from 1 , 2 , 3 are 1 + 2 and 2 + 3 . This means that every edge has to connect one vertex with 2 and a vertex with 1 or 3 .
If we place a 2 on vertex a , vertices b , c and d will get 1 or 3 later, but then e and f need to have a 2 and finally, g gets 1 or 3 .
If we didn't place a 2 on a , but rather on b , c , d , we would also need one on g .
So, there are 2 ways to fill in all necessary 2 's. For the other vertices, we can choose freely. In the first case, there are 2 4 = 1 6 choices and in the second 2 3 = 8 choices. This gives a total number of 1 6 + 8 = 2 4 ways.