Tessellate S.T.E.M.S - Computer Science - School - Set 1 - Problem 2

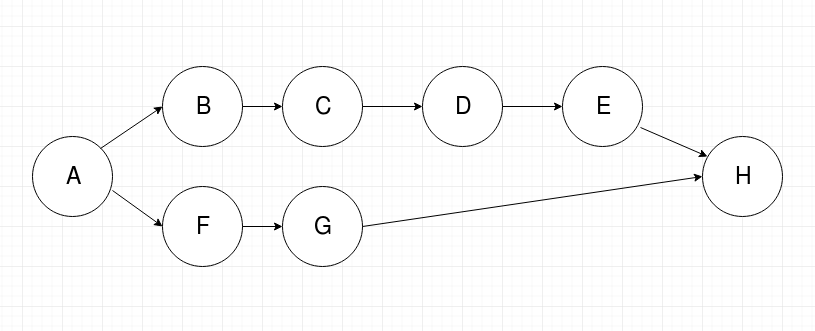
Let's write all the nodes in the dependency diagram in a linear manner, just to make it easier for analyzing:-

1_ _ _ _ 6 _ _ _ 10 where 1,2,3..... are the library numbers.

Now, since library-1 will always be installed at the very beginning, we fix it's place in the sequence (as shown above). Similarly, library-6 will always be installed after installing the first 5 libraries no matter the sequence. So we fix it's position (as shown). We do the same for library-10 as well, since it will always be installed right at the end.

Now, considering libraries between 1 and 6 - we can observe that the second library to be installed can never be 3 or 5, so we eliminate all the sequences where 3 or 5 is the second library installed. Listing out the possible sequences of libraries where library-4 was installed second:

• 1 4 2 5 3 6 _ _ _ 10 --> (A)
• 1 4 2 3 5 6 _ _ _ 10 --> (B)
• 1 4 3 5 2 6 _ _ _ 10 --> (C)
• 1 4 3 2 5 6 _ _ _ 10 --> (D)
• 1 4 5 2 3 6 _ _ _ 10 --> (E)
• 1 4 5 3 2 6 _ _ _ 10 --> (F)

Here we notice that only (A), (B) and (E) are possible i.e half of the possible sequences. Similarly, only half of all sequences are possible in the case where library-2 is installed second. Total = 6 sequences.

Considering libraries between 6 and 10 and listing out all the possible sequences independently of the order of first 6 libraries:

• 1 _ _ _ _ 6 8 7 9 10 --> (A)
• 1 _ _ _ _ 6 8 9 7 10 --> (B)
• 1 _ _ _ _ 6 9 7 8 10 --> (C)
• 1 _ _ _ _ 6 9 8 7 10 --> (D)
• 1 _ _ _ _ 6 7 8 9 10 --> (E)
• 1 _ _ _ _ 6 7 9 8 10 --> (F)

Only (C), (E) and (F) are possible. Total = 3 sequences.

Combining, we get a total of 6 * 3= 18 total possible sequences in which the library-10 can be installed.

Although this problem is quite easily done by listing all the possible cases, I tried to generalise it for any given number of libraries between two 'fixed' libraries.

I have defined a fixed library as one which is dependent on multiple libraries. (For example, libraries 6 and 10 in the given problem).

If the number of libraries between two fixed libraries is 'n', then, the number of valid sequences between these two libraries is given by $\frac{n!}{a! \times b! \times c! \times ...}$ , where a, b, c, ... are the number of libraries in each branch between the two fixed libraries.

Consider the following dependency diagram:

Here, A and H are fixed libraries.

Think of the names of the libraries as letters of a word. We want to find the number of 'valid' words.

A word is only valid if:

• C occurs after B in the word (times 1/2) [C either occurs after B, or before B, hence 1/2 cases]
• D occurs after B and C in the word (times 1/3) [D either occurs before, in between or after B and C, hence 1/3 cases]
• E occurs after B, C and D in the word (times 1/4) [Similar argument as above]
• G occurs after F in the word (times 1/2) [Similar argument as above]

(the quantity in the bracket denotes the factor by which the total number of permutations is multiplied in order for the corresponding condition to be satisfied)

then the number of words satisfying the above conditions are: $\frac{6!}{2 \times 2 \times 3 \times 4} = 15$

This result can be verified by listing all valid sequences: {BCDFGE, BCFDGE, BCFGDE, BFCDGE, BFCGDE, BFGCDE, FGBCDE, FBGCDE, FBCGDE, FBCDGE, BCDEFG, BCDFEG, BCFDEG, FBCDEG, BFCDEG}

This result is valid in general.

By finding out the number of valid sequences between multiple fixed libraries, the final answer can be obtained by multiplying them, i.e., if A, B, and C are three fixed libraries such that the number of valid sequences between A and B is 'x' and between B and C is 'y', then then number of valid sequences between A and C is 'xy' (x times y).

As for the given question,

number of valid sequences between 1 and 10 = number of valid sequences between 1 and 6 $\times$ number of valid sequences between 6 and 10

$=\frac{4!}{2!\times2!} \times \frac{3!}{2!\times1!}$

$=6 \times 3$

$=18$