Tessellate S.T.E.M.S - Physics - School - Set 3 - Problem 5
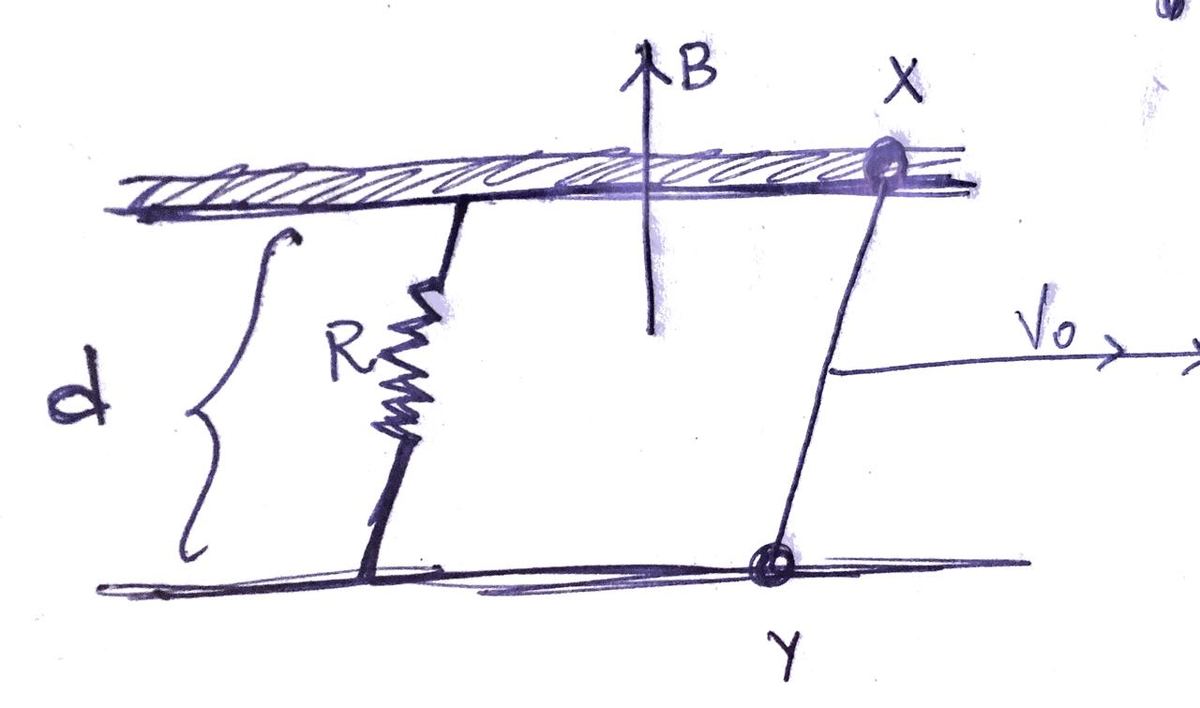
Rod ( XY ) of mass can slide without friction along two parallel horizontal rails separated by distance . Rails are connected to resistor of resistance and placed in vertical magnetic field of induction . The jumper is given velocity as shown. The distance covered by rod before it comes to rest is?
Given - kg , ohm, m/s, T, m.
This problem is a part of Tessellate S.T.E.M.S.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The rate at which the rod's kinetic energy is lost is equal to the rate at which thermal energy is dissipated in the resistor. Call the induced voltage ϵ and the bar speed v .
Induced voltage:
ϵ = B d v
Resistor power:
P R = R ϵ 2 = R B 2 d 2 v 2
Bar kinetic energy:
E = 2 1 m v 2
Rate of change of bar kinetic energy:
d t d E = d v d E d t d v = m v d t d v
Equating the two:
P R = − d t d E R B 2 d 2 v 2 = − m v d t d v d t d v = − m R B 2 d 2 v
From here on, the problem can be easily solved numerically. It can also be solved analytically, as desired.
Addendum (analytical solution):
We can remove time from the equation by applying the chain rule to our result.
d t d v = − m R B 2 d 2 v d x d v d t d x = − m R B 2 d 2 d t d x d x d v = − m R B 2 d 2 d x = − B 2 d 2 m R d v
Integrate to find the total displacement:
Δ x = − B 2 d 2 m R ∫ v 0 0 d v = B 2 d 2 m R ∫ 0 v 0 d v = B 2 d 2 m R v 0