Test

\num :

$\num{1234567890}$

$\num{12345.67890}$

---

\numcomma :

$\numcomma{1234567890}$

$\numcomma{12345.67890}$

---

---

If we're given a vector $\vec{n} = \langle a , b , c \rangle$ perpendicular to a plane and a point $\vec{P} = \langle x_{0} , y_{0} , z_{0} \rangle$ on the plane, then an equation for that plane must be $\vec{n} \cdot \big( \vec{x}-\vec{P}\big) = a(x-x_{0}) + b (y-y_{0}) + c (z-z_{0}) = 0.$

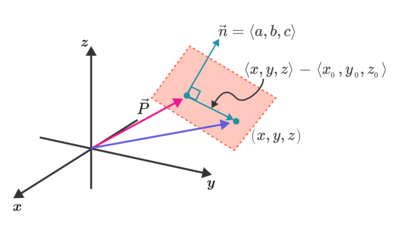
Alternatively, if we're given three non-collinear points $P,Q,$ and $R$ on a plane, then we can construct a vector perpendicular to the plane using the cross product $\vec{n} = \vec{PQ} \times \vec{PR}.$ Find an equation for the plane through the points $(1,-2,0),\ \ (5, -1,-1), \ \ \text{and} \ \ (-7,0,0)$ by first finding a unit vector $\hat{n}$ perpendicular to the plane and then using the planar equation above. Some simplification may be required. Recall that the cross product is defined by $\det \begin{pmatrix} \hat{i} & \hat{j} & \hat{k} \\ \textcolor{#3D99F6}{b}_{1} & \textcolor{#3D99F6}{b}_{2} & \textcolor{#3D99F6}{b}_{3}\\ \textcolor{#20A900}{c}_{1} & \textcolor{#20A900}{c}_{2} & \textcolor{#20A900}{c}_{3}\end{pmatrix} = \vec{\textcolor{#3D99F6}{b}} \times \vec{\textcolor{#20A900}{c}}.$

---

Note: At the end of your calculation, you might have to multiply by a constant to match our solution. If this occurs, don't worry; you just found an equivalent description of the plane!

$\Huge{\blue{x}\red{y}}$

$z \overline{z}$

$^{\deg}C$

$\LaTeX$