Testing Collatz Conjecture

Computer Science Level 3

Collatz conjecture states that take any natural number $n$ , if $n$ is even divide it by $2$ to get $n/2$ , if $n$ is odd multiply it by $3$ and add $1$ to get $3n+1$ . Repeat the process indefinitely, no matter what number you start with, you will always eventually reach $1$

Proving or disproving this conjecture is still a open problem in mathematics, but anyways here's the problem :

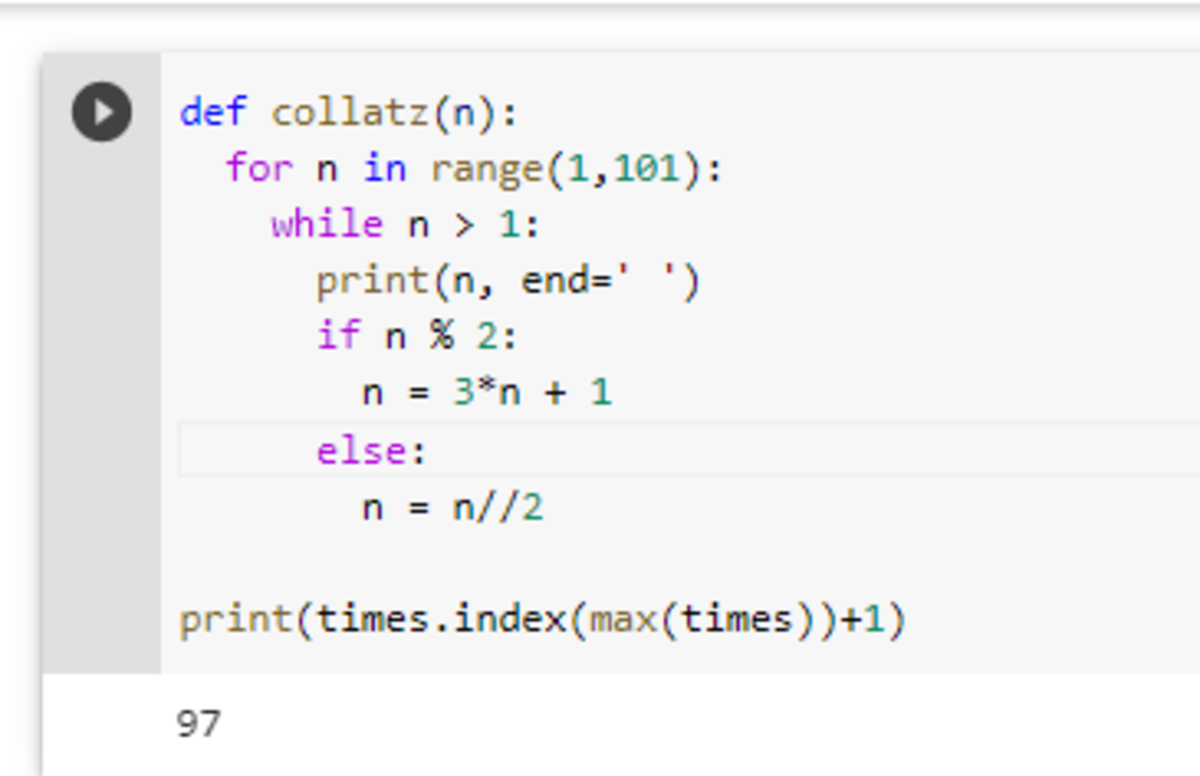
From first $100$ natural numbers, find the number which takes most number of iterations to reach $1$ (Remember we have to stop as soon as we reach to $1$ otherwise we will end in an indefinte cycle of $4-2-1$ )

As an example for number $6$ we have :

$6\rightarrow 3\rightarrow 10\rightarrow 5\rightarrow 16\rightarrow 8\rightarrow 4\rightarrow 2\rightarrow 1$

Here it is clear that $8$ iterations are involved

The answer is 97.

6 solutions

David Holcer
Apr 6, 2015

times=[]
for i in xrange(1,101):
    time=0
    while i!=1:
        if not i%2:
            i/=2
            time+=1
        else:
            i=(3*i)+1
            time+=1
    times.append(time)
print times.index(max(times))+1

:) fun

I submit most number of iterations 118 and get wrong answer.

Shohag Hossen - 5 years, 11 months ago

He is asking for the number that returns that, like 6 returns 8

Sanchit Sharma - 3 months, 3 weeks ago

This is my exact sol

Sanchit Sharma - 3 months, 1 week ago

Elijah Frank
Dec 6, 2020

Exactly how I did it!

Sanchit Sharma - 3 months, 3 weeks ago

Aryan Gaikwad
Mar 18, 2015

Java solution -

public static void main(String[] args){
    int max = 0, lar = 0;;
    for(int i = 1; i <= 100; i++)
        if(it(i) > max){
            max = it(i);
            lar = i;
        }
}

private static int it(int n){
    int a = n, i = 0;
    while(a != 1){
        if(a % 2 == 0) a /= 2;
        else a = (a * 3) + 1;
        i++;
    }
    return i;
}

Output - 97

Execution time - 0.000428869 seconds

Pranjal Jain
Mar 17, 2015

#include <stdio.h>

int main(int argc, char **argv)
{
  int longest = 0;
  int terms = 0;
  int i;
  unsigned long j;

  for (i = 1; i <= 100; i++)
  {
    j = i;
    int this_terms = 1;

    while (j != 1)
    {
      this_terms++;

      if (this_terms > terms)
      {
        terms = this_terms;
        longest = i;
      }

      if (j % 2 == 0)
      {
        j = j / 2;
      }
      else
      {
        j = 3 * j + 1;
      }
    }
  }

  printf("longest: %d (%d)\n", longest, terms);
  return 0;
}

0.004047 seconds!

Kartik Sharma
Mar 15, 2015

 def collatz(n):
    K = 0
    while n != 1:
        if n%2==0:
            n = n/2
        else:
            n = 3*n+1
        K = K + 1
    return K
 D = {}
 for i in range(1,101):
    D[i] = collatz(i)
 max(D, key=D.get)

It's from Project Euler, right?

Kartik Sharma - 6 years, 3 months ago

Yep, number 14

Try this diabolical one instead: number 494

Pi Han Goh - 6 years, 3 months ago

Raghav Vaidyanathan
Mar 15, 2015

#include<iostream.h>
#include<conio.h>
//to print number with largest stoppping time below 'n'
int main()
{
clrscr();
int *x,n,k,a=1;
cin>>n;
x=new int[n+1];
for(int i=1;i<=n;(x[i]>x[a])?a=i:a=a,i++)
    for(x[i]=0,k=i;k!=1;x[i]++)
        (k%2==0)?k/=2:k=3*k+1;
cout<<a<<" - "<<x[a];
getch();
delete []x;
return 0;
}

Testing Collatz Conjecture

The answer is 97.

6 solutions

0 pending reports