Tetherball
Consider a ball hung from rope of length l = 2 m which is attached to the top of a vertical pole. Initially, the rope is vertical and the ball is given a horizontal initial speed v 0 . What is minimum initial speed v 0 in meters per second for which the ball hits the top of the pole. Ignore friction, the mass of the rope and treat the ball as a point mass.
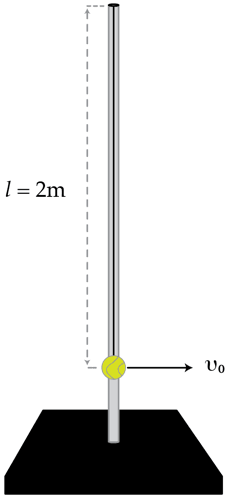
Details and assumptions
g = 9 . 8 m / s 2
The answer is 8.55.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Try conserving energy from lowest point instead and also write proj motion eqns as if down an incline of angle theta . This way you dont have to solve for theta itself . Thats how i did it
But the language of the question suggests other possible values of v0? Its asking for the minimum
Wow, that's extremely elaborate- I didn't think that far :(. My way of doing it is sort of simple, but it worked I guess. I just used conservation of energy like this: 1/2mv^2=2mgl. According to that, the ball goes to the very top and falls straight down. It gives me a value of approx. v=8.54377. I put it in as 8.55, and they called it correct, but it seems sort of strange to me... I think maybe my way is fundamentally incorrect (doesn't seem like a very efficient way of getting the ball to the top), but I got lucky in that the answer was very close. What do you think?
Log in to reply
I think your way would have worked if the velocity was pointed at the sky. However, since it is pointed horizontally, the ball would not move in a circular motion to reach to the top; it will start moving in a projectile motion after the tension of the rope is gone. I do not think it is physically possible to move a ball horizontally and goes to the very top and falls straight down, in my opinion. But maybe I am wrong haha.
I think you copied your calculator wrong because according to the way you did it the answer is supposed to be 8.854377, so I think you got lucky and missed the 8 in the tenths digit :P
Log in to reply
Oh, wow you're right! I guess I was double-incorrect :(.
Exactly the same mistake lol!
Instead of directly solving the nasty equation for theta, you can further simplify it by using the trigonometric identity s i n 2 θ + c o s 2 θ = 1 . Doing so, we obtain tan 2 θ = 2 1 . Therefore θ = arctan 2 1 ≈ 3 5 . 2 6 4 ∘ .
Log in to reply
There's another way of solving the problem without needing to solve for θ at all. Using the result t a n 2 θ = 2 1 above, we obtain s i n 2 θ = 3 1 . As mentioned in the comments above, the energy is conserved from the lowest point: 2 1 m v 0 2 = 2 1 m v 2 2 + m g l ( 1 + sin θ ) . Since v 2 = g l sin θ , we find that 2 1 m v 2 2 = m g ( 2 1 sin θ ) and 2 1 m v 0 2 = m g l ( 1 + 2 3 sin θ ) . Rearranging and simplifying, we get v 0 = ( 2 + 3 sin θ ) g l . Plugging in the value of l = 2 m , g = 9 . 8 m / s 2 and sin θ = 3 1 , we find the answer v 0 ≈ 8 . 5 5 2 6 m / s
Let the tension in the string be T . Boundary condition for string going slack at the top of the ball's circular trajectory is T = 0 . From this point onwards, the ball behaves like a projectile. Thus at the top of its circular trajectory (let it be called point C), making an angle θ above the horizontal with the top of the pole, where the string goes slack - T + m g s i n θ = l m v c 2 Since T = 0 m g s i n θ = l m v c 2 v c 2 = g l s i n θ . . . . ( 1 )
For the ball to strike the top of the pole, the following conditions must be met
v c s i n θ t = l c o s θ → t = v c t a n θ l . . . ( 2 )
Vertical displacement for the ball now behaving as a projectile
v c c o s θ t + 2 1 g t 2 = − l s i n θ
From (2)...
v c c o s θ ( v c t a n θ l ) + 2 1 g ( v c t a n θ l ) 2 = − l s i n θ → v c 2 [ c o s θ t a n θ + t a n θ 2 s i n θ ] = 2 g l . . . ( 3 )
Replacing value of v c 2 from (1) in (3) and cancelling terms, we get
s i n θ ( cos θ t a n θ + t a n 2 θ s i n θ ) = 2 1 → 2 s i n 2 θ c o s 2 θ + 2 s i n 4 θ = c o s 2 θ . . ( 4 )
Substituting s i n 2 θ = a we can write (4) as-
2 a ( 1 − a ) + 2 a 2 = 1 − a → a = 1 / 3 → s i n θ = 1 / 3 v c 2 = g l sin θ = g l 3 1 . . . . ( 5 )
From conservation of energy we know that
v 0 2 = v c 2 + 2 g ( l + l sin θ ) = g l sin θ + 2 g ( l + l sin θ ) v 0 2 = g l ( 2 + 3 s i n θ )
From (5)..
v 0 = g l ( 2 + 3 ) = 8 . 5 5 m s − 1
Exactly...
we can first assume that the ball should have a velocity to at least reach to the same height (but not hitting) as the top of the pole. So for the sake of simplicity, let's say the velocity of the ball when the ball comes to the same height as the top of the pole v 1 .
Then, the key of this problem is the change from circular motion to a projectile motion . At the beginning, since there was a tension at the rope that forces the ball not to go outward the natural length of the rope, the ball was forced to move in a circular motion. However, when the ball goes upward, the tension force starts to decrease because the gravitational force is replacing it for the centripetal force of the ball, and at certain point, when the portion of the gravitational force equals to the centripetal force, the tension force equals to zero and the ball starts to move in a projectile motion. Here is a primitive picture for better understanding. Let's say the angle between the horizontal line at the top of the pole and the rope when the ball starts to move in a projectile motion θ and the velocity of the ball when it starts to move in a projectile motion v 2 .
Then, by the conservation of energy, we can write 2 1 m v 1 2 = m g l sin ( θ ) + 2 1 m v 2 2
Also, the portion of the gravitational force must equal to the centripetal force, so m g sin ( θ ) = l m v 2 2
By simplifying these two equations, we can get v 2 2 = g l sin ( θ ) = v 1 2 − 2 g l sin ( θ )
Then, now let's go to the projectile motion part. The horizontal displacement function of the ball to hit the top of the pole will be x = v 2 sin ( θ ) t = l cos ( θ )
Similarly, the vertical displacement will be y = v 2 cos ( θ ) t − 2 1 g t 2 = − l sin ( θ )
then, we can substitute t into t = v 2 sin ( θ ) l cos ( θ ) to the vertical displacement. Also, by changing v 2 2 into g l sin ( θ ) , sin ( θ ) cos 2 ( θ ) ( 1 − 2 sin 2 ( θ ) 1 ) = − sin ( θ )
It is a pity that I was not able to solve this equation nicely, so I used the calculator. Thus, the angle was θ = 3 5 . 2 6 4 .
Then, we can plug this value into g l sin ( θ ) = v 1 2 − 2 g l sin ( θ ) and get the value of v 1 . Thus, the velocity value was v 1 = 5 . 8 2 6 5 .
Finally, we can find the value of v 0 , the velocity of the ball at the bottom of the pole. By the conservation of energy, 2 1 m v 0 2 = m g l + 2 1 m v 1 2 Then, the answer is v 0 = 8 . 5 5 0
Note: if someone has a better solution without solving such nasty equation above, I would be very pleased.