Tetherball
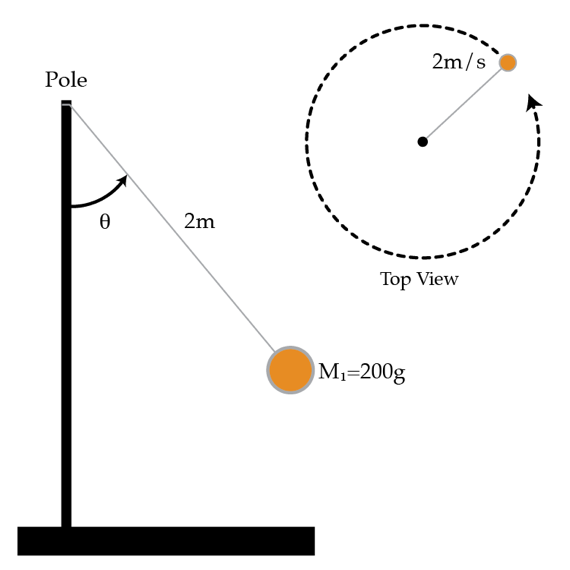
Tetherball is a game played by kids. The equipment consists of a volleyball on a string, with the other end of the string tied to the top of a post. Kids hit the ball back and forth around the post. Consider a volleyball of total mass 200 g attached to the top of a post by a 2 m long cord. The volleyball is traveling in a horizontal circle with a speed of 2 m/s. What is the angle θ between the post and the cord in degrees ?
Details and assumptions
- The acceleration of gravity is − 9 . 8 m/s 2 .
The answer is 25.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
The forces acting on the ball are : 1. The gravitational force acting vertically downwards 2. The centrifugal force acting radially outwards 3. The tension in the string
The ball will maintain a particular angle when the tension in the string balances the resultant of the remaining two.
Equating the component gives: T cos θ = m g T sin θ = r m v 2
Dividing the second equation by the first gives tan θ = r g v 2
r = l sin θ
where l is the length of the string.
Substituting the values give cos θ sin 2 θ = 4 . 9 1 which on solving gives the required answer.
Let the mass of the ball be m , let the acceleration due to gravity be g , let the velocity of the ball be v , let the tension of the string be T , let the length of the string be l . The numerical values will be put later.
We can resolve T into 2 components, the horizontal component which is T s i n θ [pointing inwards] and the vertical component which is T c o s θ [pointing upwards]. Now let the horizontal distance from the pole to the ball be r , so r = l s i n θ . Then the centrifugal force acting on the ball will be m v 2 / r = m v 2 / l s i n θ [directed outwards]. The gravitational force acting on the ball will be m g [directed downwards]. Thus equating...
T c o s θ = m g . . . . . ( 1 ) T s i n θ = m v 2 / l s i n θ . . . . . ( 2 )
Divide equation (1) from equation (2)...
t a n θ = v 2 / l g s i n θ ⟹ s i n 2 θ / c o s θ = v 2 / g l . Solving for θ gives θ = a r c c o s ( ( s q r t ( ( g l ) 2 + 4 ) − g l ) / 2 ) [The other solution can automatically be rejected since it is negative. Also note that this solution is always positive for all real values of g and l ]. Plugging the numerical values gives θ 2 5 . 4 ∘ .
weight of ball =
m
∗
g
radius of motion,
r
=
2
sin
θ
centripetal force,
F
c
=
m
g
∗
tan
θ
F
c
=
m
g
∗
tan
θ
=
r
m
∗
v
2
cos
θ
g
sin
2
θ
=
2
sin
θ
2
2
g
(
1
−
cos
2
θ
)
=
2
cos
θ
0 = g \cos^2 \theta +2 \cos \theta -g
Solving for
cos
θ
,
cos
θ
=
0
.
9
0
1
5
1
8
6
5
o
r
−
1
.
1
0
7
2
3
3
(
N
.
A
)
therefore
θ
=
2
5
.
4
∘
The centripetal acceleration of the ball around the post is a = v 2 / ( L sin θ ) = 2 / sin θ . The necessary force for this motion is supplied by the horizontal component of the tension T in the string, i.e. F h = T sin θ . The vertical component of the tension counteracts the force of gravity, so T cos θ = m g . We therefore have m g tan θ = 2 m / sin θ , and can hence solve for
cos θ sin 2 θ = g 2 . This equation can be solved by replacing sin 2 θ = 1 − cos 2 θ , and applying the quadratic formula (using c o s θ as the variable) to find that θ = 2 5 . 4 ∘ .
T cos(x)=mg, T sin(x)=v*v/2 sin(x), x is angle which we have to calculate, T is tension in string ,
This problem may be solved by applying Newton's Laws of motion to a system in dynamic equilibrium, through the assistance of a free body diagram. Let us define the system to be the ball.
In equilibrium, the vertical velocity of the ball is zero, while the horizontal velocity is constant at v = 2 m/s. Therefore the only forces acting on the ball are gravity ( m g ) in the vertical downward direction and force due to tension ( T ) in the direction of the string, defined by the angle as diagrammed.
Therefore the net acceleration in the vertical direction is zero, and the net acceleration in horizontal direction is constant, as given by the centripetal acceleration of a = r v 2 . Now describe the sum of the forces in each independent direction, given each respective net acceleration.
In the x-direction:
T x = T sin ( θ ) = r x m v 2 = r sin ( θ ) m v 2 , where r x = r sin ( θ ) is the horizontal radius of curvature for the orbiting ball, and r = 2 m is the total length of the string.
In the y-direction:
T y = T cos ( θ ) + m g = 0 , T y = T cos ( θ ) = − m g , where g = − 9 . 8 m/s 2 is defined positive in the upward direction.
Now solve for θ by dividing the two equations.
T cos ( θ ) T sin ( θ ) = m g r sin ( θ ) − m v 2 , cos ( θ ) sin 2 ( θ ) = g r − v 2 .
Let x = cos ( θ ) and ( 1 − x 2 ) = sin 2 ( θ ) .
x 1 − x 2 = g r − v 2 , which may now be solved as a quadratic equation.
x 2 − g r v 2 x − 1 = 0 ,
where the unitless quantity g r v 2 = ( − 9 . 8 ) ( 2 ) 2 2 = − 4 . 9 1 .
x = 2 − 4 . 9 1 ± ( 4 . 9 1 ) 2 − 4 ( 1 ) ( − 1 ) ≈ 0 . 9 0 3 1 5 and − 1 . 1 0 7 2 .
Disregard negative solution. Therefore θ = cos − 1 ( x ) = 2 5 . 4 2 ∘ .
One interesting note is that the solution is mass independent.