Tetra Modulus

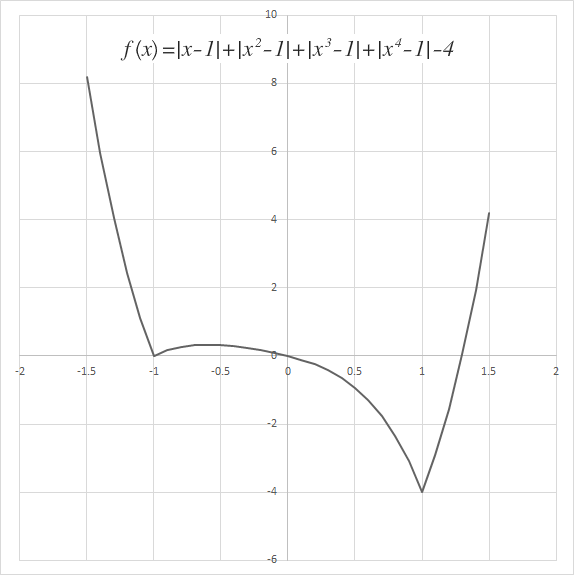
Let $f(x) = |x-1| + |x^2 - 1| + |x^3 - 1| + |x^4 - 1|$ . The easiest way to solve these kinds of problems is by reducing the study of the function to an interval or set of intervals where the function behaves nicely. We may start by observing that $f(2) > 4$ and $f(-2) > 4$ to reduce the problem to studying the function in $(-2,2)$ . Now, evaluating at every other integer in this interval we get $f(-1) = 4, f(0) = 4, f(1) = 0$ . This already gives two solutions.

In the interval [-2,-1) $f(x) > f(-1) = 4$ so no roots will be here. In the interval $(-1,0)$ each of the terms inside the absolute values will be negative so in this interval the function will be behave like $(1 - x) + (1-x^2) + (1 - x^3) + (1 - x^4) = 4 - x - x^2 - x^3 - x^4$ . Solving $4 - x - x^2 - x^3 - x^4 = 4$ we obtain the solutions $x=0, x=-1$ which we already knew. In $(0,1)$ again all the terms inside the absolute values will be negative so we get the same function as before, which will give us no new solutions. Finally, in the interval $(1,2)$ all the terms inside the absolute values will be positive so locally the function will behave like $(x-1) + (x^2 - 1) + (x^3 - 1) + (x^4 - 1) = x + x^2 + x^3 + x^4 - 4$ and solving $x + x^2 + x^3 + x^4 - 4 = 4$ actually yields two solutions that are approximately $1.2975$ and $-1.9060$ but as we are studying an specific interval, the only solution that is also valid for $f$ is $1.2975$ . This a third solution and all the intervals that could possibly contain solutions have been checked, so there are not any other solutions.

Let $f(x) = |x-1| + |x^2-1| + |x^3-1| + |x^4-1| - 4$ . We need to find the number of real solutions for $f(x) = 0$ . Then we have:

$f(x) = \begin{cases} -x+1 + x^2-1 - x^3+1 + x^4-1 - 4 = x^4 - x^3 + x^2 - x - 4 & \text{for } x < -1 & \implies f(x) < 0 & \color{#D61F06} \text{0 solution} \\ -x+1 - x^2+1 - x^3+1 - x^4+1 - 4 = -x^4 - x^3 - x^2 - x & \text{for } - 1 \le x < 1 & \implies f(-1)=f(0) = 0 & \color{#3D99F6} \text{2 solutions} \\ x-1 + x^2-1 + x^3-1 + x^4-1 - 4 = x^4 + x^3 + x^2 + x - 8 & \text{for } x \ge 1 & \implies f(x) = 0 \text{ when }x \approx 1.297526 & \color{#3D99F6} \text{1 solution} \end{cases}$

Therefore, the number of real solutions is $\boxed{3}$ .