Tetrahedral Slice
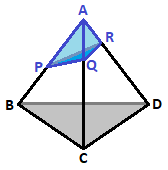
Regular tetrahedron is cut by a plane such that a new, irregular tetrahedron is formed.
If the area of is , the area of is , and the area of is , find the volume of tetrahedron .
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let p = ∣ ∣ A P ∣ ∣ , q = ∣ ∣ A Q ∣ ∣ , r = ∣ ∣ A R ∣ ∣ . Using basic trigonometry, we find that the area of Δ A P R is sin ( 3 π ) 2 p r = 4 3 p r . Writing analogous equations for the other two triangles and multiplying them together, we find that ( 4 3 ) 3 ( p q r ) 2 = 1 0 3 ( 1 4 2 − 6 1 ) so p q r = 1 2 0 2 . Finally, scaling the volume formula V = 6 2 a 3 for a regular tetrahedron, we can conclude that V = 6 2 p q r = 2 0 .
A charming and very well-crafted problem! Thank you for sharing!