tetrahedron
Geometry
Level
pending
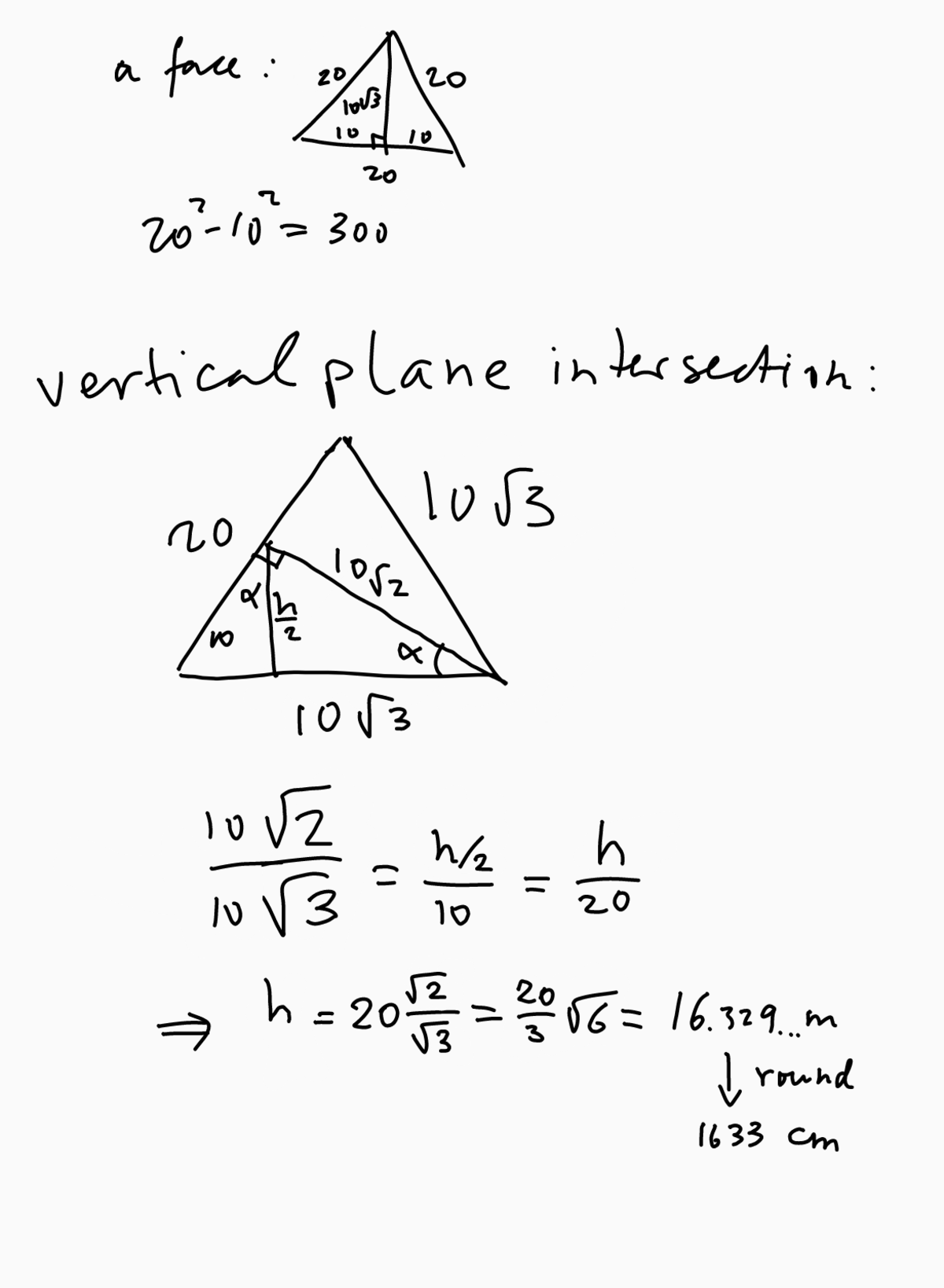
Find the height of a tetrahedron with edges of 20m. Round to the nearest cm.
The answer is 1633.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A tetrahedron has equilateral triangles for faces. A vertical plane of symmetry runs through the top, and one of the other vertices, and perpendicular through the middle of the edge that connects the other two vertices. In this plane we get a new (isosceles) triangle with sides: 2 0 , 1 0 3 , 1 0 3 . The shorter sides correspond to the height of a face.
By using pythagoras and using similar triangles, we find the height, see figure