Tetrahedrons!

In △ A B C , the inscribed circle with radius r is tangent to A B , B C and A C at points D , E and F respectively.
Folding the arc of the semi-circle at a right angle, as shown below, the radius of the semicircle becomes the height of the tetrahedron.

Let S be the total surface area of the tetrahedron.
If A △ A B C = r ( 2 1 2 r 2 + 1 1 8 8 ) and A △ A B C S = α + β , where α and β are coprime positive integers, find α + β .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Of course this would be true for any triangle with inscribed circle whose height of the tetrahedron is equal to the radius of the circle. I should have asked for the total surface area, in which case you at least needed to obtain the radius of the circle and the perimeter of the triangle using the given information. I had most of the work done from a previous problem and just quickly did the rest of the solution.
Log in to reply
I didn't think you intended for this shortcut! You could post a new similar question where it asks for the total surface area instead (as you said).
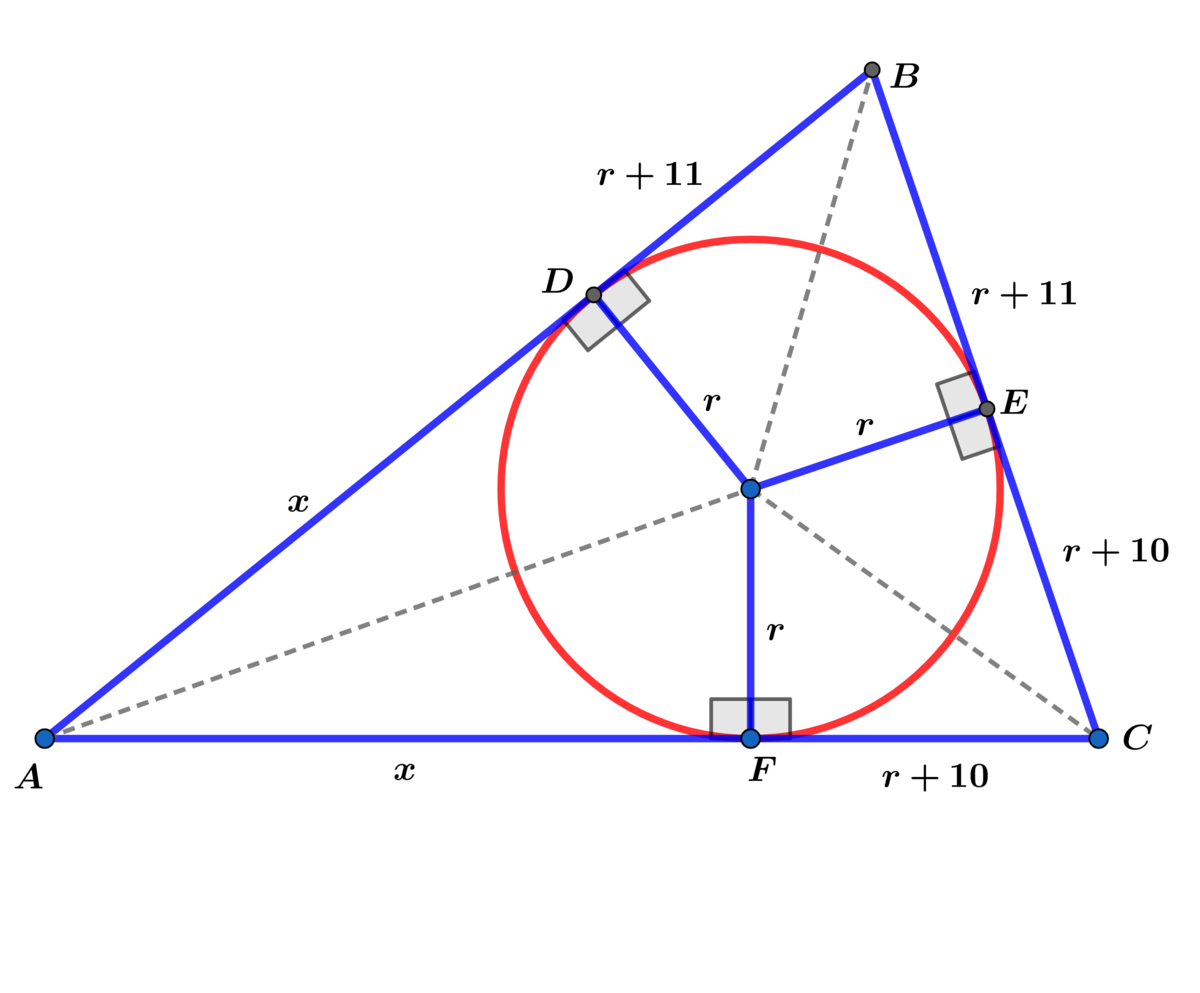
A △ A B C = 2 1 ( x + r + 1 0 ) r + 2 1 ( x + r + 1 1 ) + 2 1 ( 2 r + 2 1 ) = ( x + 2 r + 2 1 ) r
and using Heron's formula with s = x + 2 r + 2 1 ⟹
A △ A B C = ( x + 2 r + 2 1 ) ( x ) ( r + 1 0 ) ( r + 1 1 ) ⟹
( x + 2 r + 2 1 ) 2 r 2 = ( x + 2 r + 2 1 ) ( x ) ( r + 1 0 ) ( r + 1 1 ) ⟹
( x + 2 r + 2 1 ) r 2 = ( r + 1 0 ) ( r + 1 1 ) x ⟹ r 2 x + ( 2 r + 2 1 ) r 2 = ( r + 1 0 ) ( r + 1 1 ) x
⟹ ( 2 1 r + 1 1 0 ) x = ( 2 r + 2 1 ) r 2 ⟹ x = 2 1 r + 1 1 0 ( 2 r + 2 1 ) r 2 ⟹
A △ A B C = ( 2 r + 2 1 ) ( 2 1 r + 1 1 0 r 2 + 1 ) r = 2 1 r + 1 1 0 ( 2 r + 2 1 ) ( r 2 + 2 1 r + 1 1 0 ) r =
r ( 2 1 2 r 2 + 1 1 8 8 ) ⟹ 4 2 r 3 + 1 3 2 3 r 2 + 1 3 8 8 1 r + 4 8 5 1 0 = 4 2 r 3 + 2 2 0 r 2 + 2 4 9 4 8 r + 1 3 0 6 8 0
⟹ 1 1 0 3 r 2 − 1 1 0 6 7 r − 8 2 1 7 0 = 0 dropping the negative root
⟹ r = 2 2 0 6 1 1 0 6 7 + 2 2 0 2 3 = 2 2 0 6 3 3 0 9 0 = 1 5 ⟹ x = 2 7 ⟹
A △ A B C = ( x + 2 r + 2 1 ) r = ( 7 8 ) ( 1 5 ) = 1 1 7 0 .
Below I use the vector cross product to find the lateral surface area, but first I need to find B ( x ∗ , y ∗ ) .

x ∗ 2 + y ∗ 2 = 2 8 0 9
( x ∗ − 5 2 ) 2 + y ∗ 2 = 2 6 0 1
⟹
x ∗ 2 − 1 0 4 x ∗ + 2 7 0 4 + y ∗ 2 = 2 6 0 1
x ∗ 2 + y ∗ 2 = 2 8 0 9
⟹ 1 0 4 x ∗ = 2 9 1 2 ⟹ x ∗ = 2 8 ⟹ y ∗ = 4 5 ⟹ B ( 2 8 , 4 5 , 0 )
A P = 2 7 i + 1 5 j + 1 5 k and A C = 5 2 i + 0 j + 0 k ⟹
⟹ A P X A C = 0 i + 7 8 0 j − 7 8 0 k ⟹ ∣ A P X A C ∣ = 7 8 0 2
⟹ A A P C = 2 1 ∣ A P X A C ∣ = 2 7 8 0 2
Similarly A B = 2 8 i + 4 5 j + 0 k ⟹ A P X A B = − 6 7 5 i + 4 2 0 j + 7 9 5 k
⟹ ∣ A P X A B ∣ = 7 9 5 2 ⟹ A A P B = 2 1 ∣ A P X A B ∣ = 2 7 9 5 2
and
C P = − 2 5 i + 1 5 j + 1 5 k and C B = − 2 4 i + 4 5 j + 0 k ⟹
C P X C B = − 6 7 5 i − 3 6 0 j − 7 6 5 k ⟹ ∣ C P X C B ∣ = 7 6 5 2 ⟹
A C P B = 2 1 ∣ A P X A B ∣ = 2 7 6 5 2
⟹ L . S . = 1 1 7 0 2 ⟹ S = 1 1 7 0 ( 2 + 1 ) ⟹ A △ A B C S = 2 + 1 =
α + β ⟹ α + β = 3 .
Let the center of the incircle be I , let the top of the tetrahedron be G , let A B = c , A C = b , and B C = a , and let the semiperimeter of △ A B C be s .
Then I G = I D = I E = I F = r , G D = G E = G F = 2 r , so A △ B C G = 2 2 a r , A △ A C G = 2 2 b r , and A △ A B G = 2 2 c r .
Since A △ A B C = r s , the surface area S = 2 2 a r + 2 2 b r + 2 2 c r + r s = 2 1 ( a + b + c ) r 2 + r s = r s 2 + r s = r s ( 2 + 1 ) .
That means A △ A B C S = r s r s ( 2 + 1 ) = 2 + 1 , so α = 2 , β = 1 , and α + β = 3 .