Tetromino Grid!!
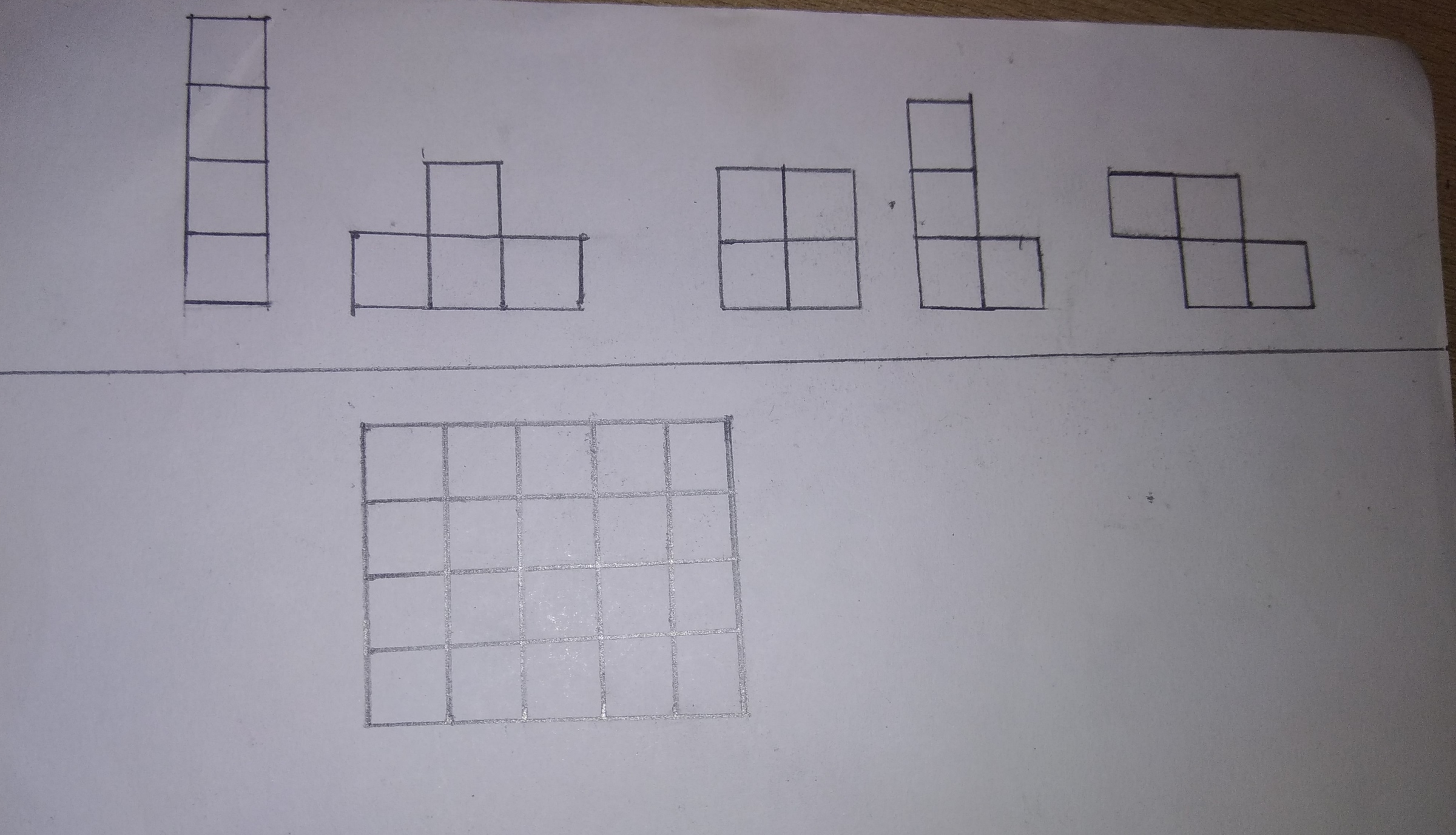
Find the number of ways of arranging the above five types of tetro-minoes in a 5×4 grid using each piece exactly once. A square in the grid can be occupied by atmost one piece.
This question is not original .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Here is an observation
Let's colour each square in the grid alternatively by White and black like a chess board.
So, we'll have an equal number of white and black squares.
So, similarly we also have to colour have each square of the tetro-minoes alternatively white and black.
So, we can see that combining all tetro-minoes, we get unequal number of black and white squares.
So, they can't fit neatly in the grid.
So, there are 0 ways.