Tetrominos to Rectangles

Geometry Level 2

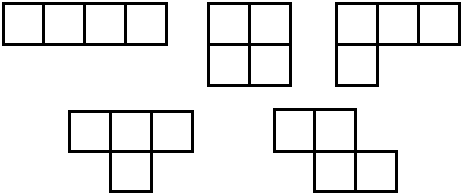
Below are five free tetrominos "I", "O", "L", "T", and "Z".

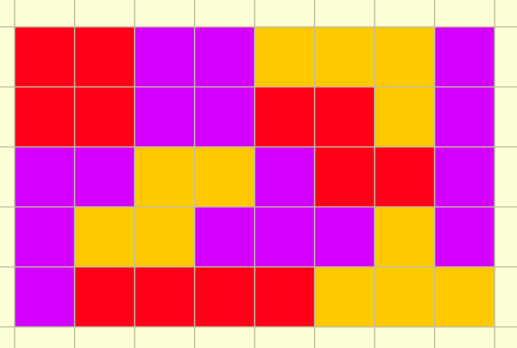
What is the minimum number of complete sets of these tetrominos (each set contains all five of them) needed to form a rectangle without gaps?

Rotation and reflections are allowed.

If it will never form a rectangle, no matter the number of sets, enter the answer as 0 0 .


The answer is 2.

Wind Quotidian by Wind Quotidian , 20, Malaysia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Stephen Mellor
Dec 21, 2017

If we consider a chess board colouring, it is obvious that the I,O,L and Z tetrominos each cover 2 white and 2 black squares. However, the T tetromino covers 3 of one colour and 1 of the other. A rectangle must have the same number of black and white squares, meaning 1 complete set isn't possible.

2 complete sets are possible, as shown below (note that this design isn't unique)

1 Helpful 1 Interesting 0 Brilliant 0 Confused

My solution involved a chess board colouring as well.

I noted that a rectangle with both odd sides (such as 3x3) must have one more square of one colour than the other, but not two.

Of course, since the set of 5 tetrominos contains 20 squares, we can't form a rectangle with both sides odd, so your solution is valid.

Steven Perkins - 3 years, 5 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...