Tetrominos
Probability
Level
5
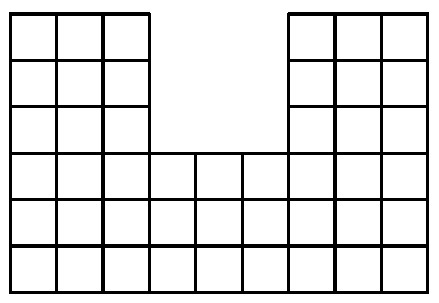 The above figure of 45 squares can be covered completely with eleven L-tetrominos and one monomino. How many possible positions are there for the position of the monomino?
The above figure of 45 squares can be covered completely with eleven L-tetrominos and one monomino. How many possible positions are there for the position of the monomino?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Label the lower left square ( 1 , 1 ) and the upper right square ( 9 , 6 ) .
Consider the coloring where we color every odd row blue. There are 24 cells that are blue. Notice that no matter where we place a L-tetromino, it must cover an odd number of blue cells. Since we use 11 L-tetrominos, this implies that they will only cover an odd number of blue cells. Hence, the monomino must cover a blue cell.
Consider the coloring where we color every even column red. There are 18 cells that are red. Similar to the argument above, the monomino must cover a red cell.
We can check that if the monomino is at ( 2 , 1 ) , then there is no way to fill up the first three columns. Hence ( 2 , 1 ) and ( 8 , 1 ) are not valid.
We can check that if the monomino is at ( 2 , 3 ) , then there is no way to fill up the first three columns. Hence ( 2 , 3 ) and ( 8 , 3 ) are not valid.
We can check that the remaining 6 positions are valid in the following way: