AM and GM
a , b , and c follow an arithmetic progression . Denote x as the geometric mean of a and b , and y the geometric mean of b and c .
Find the arithmetic mean of x 2 and y 2 in terms of a , b , and/or c .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let d be the common difference for these terms. You get a , a + d , a + 2 d by the definition of AP.
⟹ x = ( a ) ( a + d ) = a 2 + a d
⟹ y = ( a + d ) ( a + 2 d ) = a 2 + 2 d 2 + 3 a d
2 x 2 + y 2 = 2 x 2 a 2 + a d + y 2 a 2 + 2 d 2 + 3 a d = 2 2 a 2 + 4 a d + 2 d 2 = ( a + d ) 2 = b 2
@Skanda Prasad , i LOVE your description :)
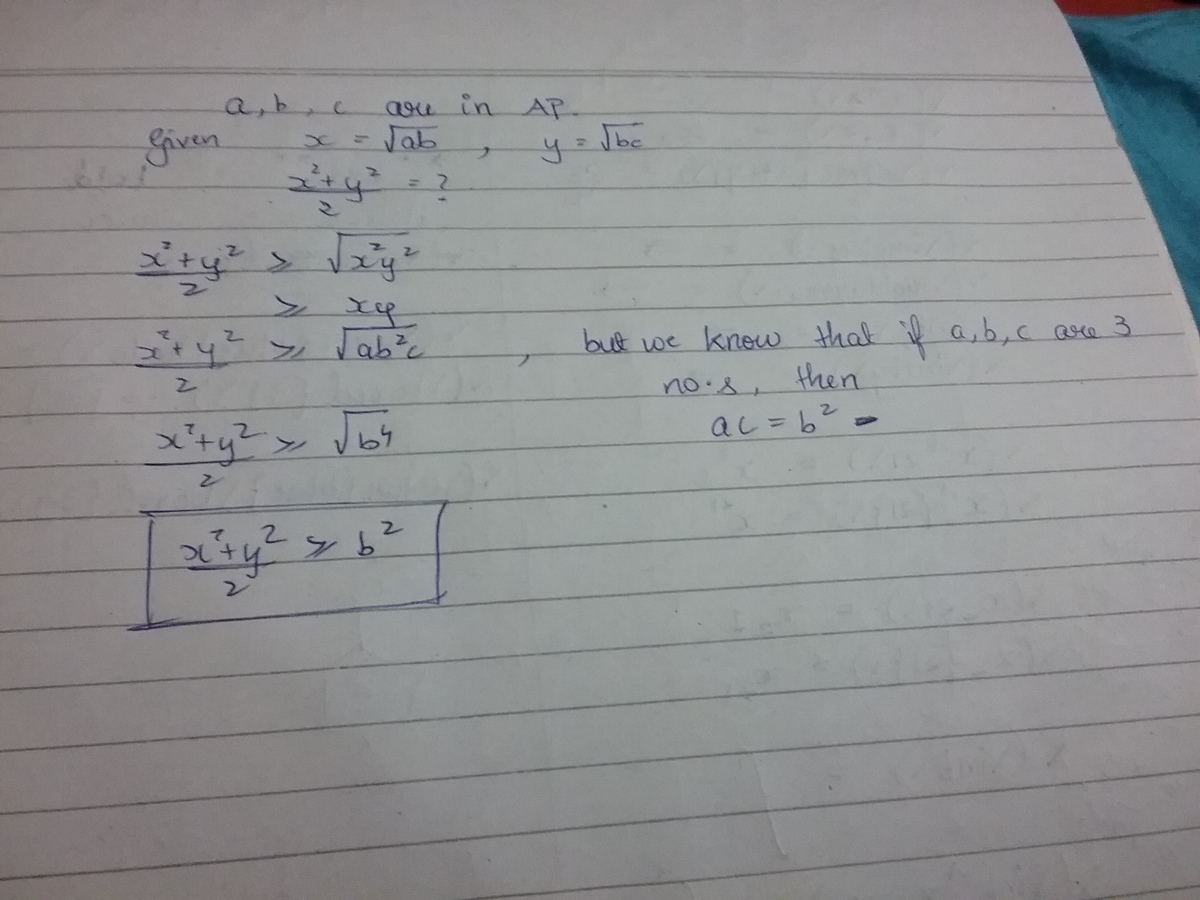
x is the geometric mean between a and b ⟹ x 2 = a b
y is the geometric mean between b and c ⟹ y 2 = b c
a , b , c are in A.P ⟹ 2 b = a + c
A.M of x 2 , y 2 = 2 x 2 + y 2
⟹ 2 a b + b c = 2 b ( a + c ) = 2 b × 2 b = b 2